题目内容
4．
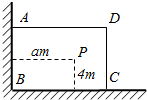如图，有-直角墙角，两边的长度足够长，在P处有-棵树与两墙的距离分别是a米（0＜a＜12），4米，不考虑树的粗细，现在想用16米长的篱笆，借助墙角围成-个矩形的花围ABCD，并要求将这棵树围在花圃内或在花圃的边界上．设BC=x米，此矩形花围的面积为y平方米．（1）写出y关于x的函数关系，并指出这个函数的定义域；
（2）当BC为何值时，花圃面积最大？
分析 （1）要使树被圈进去，则ABCD中BC≥a，CD≥4，由此可确定函数的变量的范围．设长BC=x米，宽CD=（16-x）米，所以面积y=f（x）=x（16-x）=-x2+16x；
（2）由（1）得，y=f（x）=-x2+16x=-（x-8）2+64，x∈[a，12]，由于对称轴x=8，根据0＜a＜12，故要进行分类讨论：即8≤a＜12；4≤a＜8；0＜a＜4，从而可求y=f（x）的最大值．
解答 解：（1）要使树被圈进去，则ABCD中BC≥a，CD≥4，
因为篱笆长为16米，所以当长BC=x米时，宽CD=（16-x）米．
由于BC≥a，CD≥4，故a≤x≤12，
所以面积y=f（x）=x（16-x）=-x2+16x，其定义域为x∈[a，12]；
（2）由（1）得，y=f（x）=-x2+16x=-（x-8）2+64，x∈[a，12]
对称轴x=8，又因为0＜a＜12，
所以，当8≤a＜12时，x=a时，ymax=-a2+16a；
当4≤a＜8时，x=8时，ymax=64；
当0＜a＜4时，x=8时，ymax=64．
点评 本题以实际问题为载体，考查函数模型的构建，考查二次函数最值的求解，解题的关键是读懂题意，正确分类．
练习册系列答案
相关题目
12．把一副标准的三角板按如图所示进行摆放，则AE：BE的值为（ ）
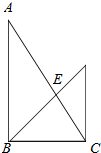
| A． | $\sqrt{3}$：$\sqrt{2}$ | B． | $\sqrt{2}$：1 | C． | $\sqrt{3}$：1 | D． | 2：1 |
16．设函数f′（x）是函数f（x）的导函数，x∈R时，f′（x）+f（x）＞0，则x1＜x2，结论正确的是（ ）
| A． | e${\;}^{{x}_{2}}$f（x1）＞e${\;}^{{x}_{1}}$f（x2） | B． | e${\;}^{{x}_{2}}$f（x1）＜e${\;}^{{x}_{1}}$f（x2） | ||
| C． | e${\;}^{{x}_{1}}$f（x1）＞e${\;}^{{x}_{2}}$f（x2） | D． | e${\;}^{{x}_{1}}$f（x1）＜e${\;}^{{x}_{2}}$f（x2） |