题目内容
16.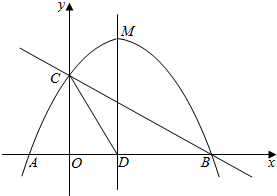 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).(1)求抛物线的解析式;
(2)判断△ACD的形状,并说明理由;
(3)在抛物线对称轴上是否存在一点P,使得△PBC是以P为直角顶点的直角三角形,若存在,求点P的坐标;若不存在,说明理由.
分析 (1)由待定系数法建立二元一次方程组求出求出m、n的值即可;
(2)求出AD=CD,即可得出结论;
(3)利用PB⊥PC,P在抛物线上,即可得出结论.
解答 解:(1)∵抛物线y=-$\frac{1}{2}$x2+mx+n经过A(-1,0),C(0,2),
∴-$\frac{1}{2}$-m+n=0,n=2
解得:m=$\frac{3}{2}$,n=2,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(2)对称轴为x=$\frac{3}{2}$,∴D($\frac{3}{2}$,0),
∴AD=$\frac{5}{2}$,AC=$\sqrt{5}$,CD=$\sqrt{\frac{9}{4}+4}$=$\frac{5}{2}$,
∴AD=CD,
∴△ACD是等腰三角形;
(3)设P(x,y),则
∵C(0,2),B(4,0),PB⊥PC
∴$\frac{y-2}{x}•\frac{y}{x-4}$=-1,
∴x(x-4)+y(y-2)=0
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,
∴x(x-4)+(-$\frac{1}{2}$x2+$\frac{3}{2}$x+2)(-$\frac{1}{2}$x2+$\frac{3}{2}$x)=0,
∴x=2,
∴y=3,∴存在一点P(2,3),使得△PBC是以P为直角顶点的直角三角形.
点评 本题考查了待定系数法求二次函数的解析式的运用、等腰三角形的性质的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.下列命题错误的是( )
| A. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
11.已知圆O1:x2+y2-4x+4y-41=0,圆O2:(x+1)2+(y-2)2=4,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
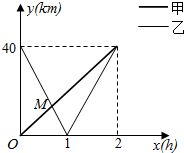 在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: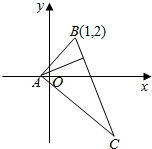 如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:
如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求: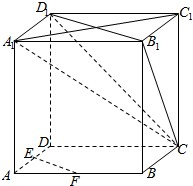 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.