题目内容
7.如图,边长为a的正方形最长的网格中,设椭圆C1,C2,C3的离心率分别为e1,e2,e3,则( )
| A. | e1=e2<e3 | B. | e1<e2=e3 | C. | e1=e2>e3 | D. | e2=e3<e1 |
分析 根据图形,利用椭圆的离心率计算公式即可得出结论.
解答 解:先看椭圆C1,长轴2a1=4a,短轴2b1∈(2a,4a),
∴离心率e1=$\frac{{c}_{1}}{{a}_{1}}$=$\sqrt{1-(\frac{{b}_{1}}{{a}_{1}})^{2}}$∈(0,$\frac{\sqrt{3}}{2}$).
椭圆C2,长轴2a1=8a,短轴2b2=4a,
∴离心率e2=$\frac{{c}_{2}}{{a}_{2}}$=$\sqrt{1-(\frac{{b}_{2}}{{a}_{2}})^{2}}$=$\frac{\sqrt{3}}{2}$.
同理可得椭圆C3的离心率e3=$\frac{\sqrt{3}}{2}$.
∴e1、e2、e3的关系为e1<e2=e3.
故选:B.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.甲、乙两人在一座9层大楼的地层进入电梯,若每个人直第二层开始在第一层离开电梯是等可能的,则2个人在不同楼层离开的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{8}{9}$ | D. | $\frac{7}{8}$ |
16.“x+y=3”是“x=1且y=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也必要条件 |
17.执行如图所示的程序框图,则输出S的值是( )
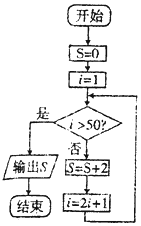

| A. | 10 | B. | 12 | C. | 100 | D. | 102 |
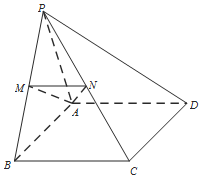 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.