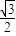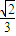题目内容
已知椭圆方程为 ,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若
,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若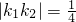 ,则椭圆的离心率为
,则椭圆的离心率为
- A.

- B.

- C.

- D.

C
分析:利用椭圆的标准方程和性质、离心率计算公式、直线的斜率计算公式即可得出.
解答:设A(a,0),B(a,0),M(x0,y0),∵M,N是椭圆上关于x轴对称的两点,∴N(x0,-y0).
∴k1= ,
, ,
, .
.
∵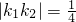 ,∴
,∴ =
= .
.
∴椭圆的离心率e= =
= =
= =
= .
.
故选C.
点评:熟练掌握椭圆的标准方程和性质、离心率计算公式、直线的斜率计算公式是解题的关键.
分析:利用椭圆的标准方程和性质、离心率计算公式、直线的斜率计算公式即可得出.
解答:设A(a,0),B(a,0),M(x0,y0),∵M,N是椭圆上关于x轴对称的两点,∴N(x0,-y0).
∴k1=
 ,
, ,
, .
.∵
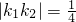 ,∴
,∴ =
= .
.∴椭圆的离心率e=
 =
= =
= =
= .
.故选C.
点评:熟练掌握椭圆的标准方程和性质、离心率计算公式、直线的斜率计算公式是解题的关键.

练习册系列答案
相关题目
 (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且 =1,|OF|=1.
=1,|OF|=1. (a>b>0),它的一个顶点为M(0,1),离心率e=
(a>b>0),它的一个顶点为M(0,1),离心率e= ,
, ,求△AOB面积的最大值。
,求△AOB面积的最大值。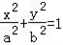 (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且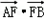 =1,|OF|=1.
=1,|OF|=1. (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且 =1,|OF|=1.
=1,|OF|=1.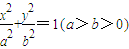 ,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若
,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若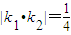 ,则椭圆的离心率为( )
,则椭圆的离心率为( )