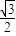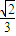题目内容
已知椭圆方程为 (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且 =1,|OF|=1.
=1,|OF|=1.
(1)求椭圆方程;
(2)直线l交椭圆于P、Q两点,问:是否存在直线l,使点F恰为△PQM的垂心?若存在,求出直线l的方程,若不存在,请说明理由.
解:(1)由题意知c=1,
又 =1,
=1,
∴(a+c)•(a-c)=1=a2-c2,∴a2=2
故椭圆方程为 ;
;
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,则
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),故kPQ=1,
于是设直线l为y=x+m,与椭圆方程联立,消元可得3x2+4mx+2m2-2=0
∵ =x1(x2-1)+y2(y1-1)=0又yi=xi+m(i=1,2)
=x1(x2-1)+y2(y1-1)=0又yi=xi+m(i=1,2)
得x1(x2-1)+(x2+m)(x1+m-1)=0
即2x1x2+(x1+x2)(m-1)+m2-m=0
由韦达定理得2•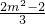 -
- (m-1)+m2-m=0
(m-1)+m2-m=0
解得m=- 或m=1(舍)
或m=1(舍)
经检验m=- 符合条件,故直线l方程为
符合条件,故直线l方程为
分析:(1)根据题意可知c,进而根据 =1求得a,进而利用a和c求得b,故可得椭圆的方程;
=1求得a,进而利用a和c求得b,故可得椭圆的方程;
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设出P,Q的坐标,利用点M,F的坐标求得直线PQ的斜率,设出直线l的方程,与椭圆方程联立,由韦达定理表示出x1+x2和x1x2,进而利用 =0求得m,即可得到直线的方程..
=0求得m,即可得到直线的方程..
点评:本题考查椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了学生综合运用基础知识解决问题的能力.
又
 =1,
=1,∴(a+c)•(a-c)=1=a2-c2,∴a2=2
故椭圆方程为
 ;
;(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,则
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),故kPQ=1,
于是设直线l为y=x+m,与椭圆方程联立,消元可得3x2+4mx+2m2-2=0
∵
 =x1(x2-1)+y2(y1-1)=0又yi=xi+m(i=1,2)
=x1(x2-1)+y2(y1-1)=0又yi=xi+m(i=1,2)得x1(x2-1)+(x2+m)(x1+m-1)=0
即2x1x2+(x1+x2)(m-1)+m2-m=0
由韦达定理得2•
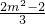 -
- (m-1)+m2-m=0
(m-1)+m2-m=0解得m=-
 或m=1(舍)
或m=1(舍)经检验m=-
 符合条件,故直线l方程为
符合条件,故直线l方程为
分析:(1)根据题意可知c,进而根据
 =1求得a,进而利用a和c求得b,故可得椭圆的方程;
=1求得a,进而利用a和c求得b,故可得椭圆的方程;(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设出P,Q的坐标,利用点M,F的坐标求得直线PQ的斜率,设出直线l的方程,与椭圆方程联立,由韦达定理表示出x1+x2和x1x2,进而利用
 =0求得m,即可得到直线的方程..
=0求得m,即可得到直线的方程..点评:本题考查椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了学生综合运用基础知识解决问题的能力.

练习册系列答案
相关题目
 (a>b>0),它的一个顶点为M(0,1),离心率e=
(a>b>0),它的一个顶点为M(0,1),离心率e= ,
, ,求△AOB面积的最大值。
,求△AOB面积的最大值。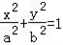 (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且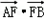 =1,|OF|=1.
=1,|OF|=1. (a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且
(a>b>0),长轴两端点A、B,短轴上端顶点为M,点O为坐标原点,F为椭圆的右焦点,且 =1,|OF|=1.
=1,|OF|=1.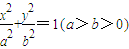 ,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若
,A、B分别是椭圆长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若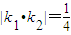 ,则椭圆的离心率为( )
,则椭圆的离心率为( )