题目内容
4．若函数f（x）=ex（x2+ax+a+1）没有极值点，则实数a的取值范围为[0，4]．分析 函数f（x）在R上没有极值点，即函数的导数等于0无解或有唯一解（但导数在点的两侧符号相同），求出函数的导数，根据二次函数的性质求得实数a的取值范围．
解答 解：函数f（x）=ex（x2+ax+a+1）在R上没有极值点，
即函数的导数等于0无解或有唯一解（但导数在点的两侧符号相同）．
而f′（x）=ex[x2+（a+2）x+2a+1]，
∴△=（a+2）2-4（2a+1）≤0，
解得：0≤a≤4，
故答案为：[0，4]．
点评 本题考查函数在某点取得极值的条件，以及方程无解或只有唯一解的条件．属于中档题．
练习册系列答案
目标测试系列答案
相关题目
15．曲线y=x3+sinx在点O（0，0）处切线方程是（ ）
| A． | y=x | B． | y=2x | C． | y=3x | D． | y=4x |
12．
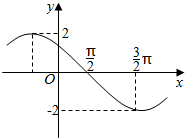已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）
已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）| A． | f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{4}$） | B． | f（x）=2sin（$\frac{1}{2}$x+$\frac{3π}{4}$） | C． | f（x）=2sin（2x-$\frac{π}{4}$） | D． | f（x）=2sin（2x+$\frac{3π}{4}$） |
19．已知直线y=kx+m（m≠0）与圆x2+y2=169有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有（ ）
| A． | 60条 | B． | 66条 | C． | 72条 | D． | 78条 |
13．函数$y=cos（-x）cos（\frac{π}{2}-x）$的最小正周期是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |