题目内容
13.已知数列{an}满足a${\;}_{n+1}^{2}$=anan+2(an≠0),0<a1<a6=1,则使不等式a1-$\frac{1}{{a}_{1}}$+a2-$\frac{1}{{a}_{2}}$+…+an-$\frac{1}{{a}_{n}}$≤0恒成立的n的最大值是11.分析 数列{an}满足a${\;}_{n+1}^{2}$=anan+2(an≠0),可得:$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n+2}}{{a}_{n+1}}$=q≠0,可得:数列{an}是等比数列.由0<a1<a6=1=${a}_{1}{q}^{5}$,可得q≠±1.a1a11=a2a10=…=a5a7=${a}_{6}^{2}$=1,n≥12时,an=${a}_{6}{q}^{n-6}$≠1.因此a1-$\frac{1}{{a}_{1}}$+${a}_{11}-\frac{1}{{a}_{11}}$=a1-$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{1}}$-a1=0=…,即可得出.
解答 解:∵数列{an}满足a${\;}_{n+1}^{2}$=anan+2(an≠0),
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{n+2}}{{a}_{n+1}}$=q≠0,
∴数列{an}是等比数列.
∵0<a1<a6=1=${a}_{1}{q}^{5}$,∴q≠±1.
∴a1a11=a2a10=…=a5a7=${a}_{6}^{2}$=1,
n≥12时,an=${a}_{6}{q}^{n-6}$≠1.
∴a1-$\frac{1}{{a}_{1}}$+${a}_{11}-\frac{1}{{a}_{11}}$=a1-$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{1}}$-a1=0,
…,
则使不等式a1-$\frac{1}{{a}_{1}}$+a2-$\frac{1}{{a}_{2}}$+…+an-$\frac{1}{{a}_{n}}$≤0恒成立的n的最大值是11.
故答案为:11.
点评 本题考查了等比数列的通项公式及其性质、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
| 频数 | 6 | 26 | x | 22 | 8 |
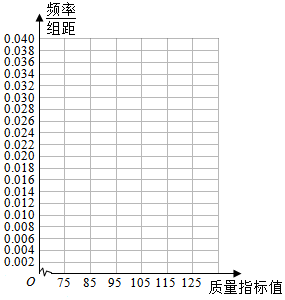
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计这种产品质量指标值的平均数$\overline{x}$及方差s2;
(3)当质量指标值位于(79.6,120.4)时,认为该产品为合格品.由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline{x}$,σ2近似为样本方差s2(每组数取中间值).
①利用该正态分布,求从该厂生产的产品中任取一件,该产品为合格品的概率;
②该企业每年生产这种产品10万件,生产一件合格品利润10元,生产一件不合格品亏损20元,则该企业的年利润是多少?
(提示:$\sqrt{104}$≈10.2,若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.6826,P(μ-2σ<Z<μ+2σ)=0.9544)
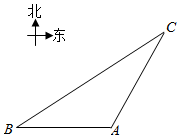 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;