题目内容
(本题满分16分)已知椭圆C的中心在原点,左焦点为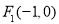 ,右准线方程为:
,右准线方程为: .
.
(1)求椭圆C的标准方程;
(2)若椭圆C上点 到定点
到定点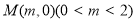 的距离的最小值为1,求
的距离的最小值为1,求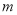 的值及点
的值及点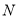 的坐标;
的坐标;
(3)分别过椭圆C的四个顶点作坐标轴的垂线,围成如图所示的矩形,A、B是所围成的矩形在 轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为
轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为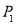 、
、 ,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形
,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形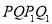 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.

(1)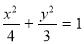 (2)
(2)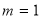 ,
,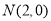 (3)四边形
(3)四边形 的面积为定值
的面积为定值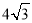
【解析】
试题分析:(1)左焦点为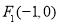 ,所以
,所以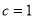 ,右准线方程为:
,右准线方程为: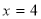
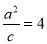 ,由此解出
,由此解出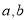 ,写出方程(2)最值问题转化为函数问题,构造
,写出方程(2)最值问题转化为函数问题,构造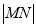 的函数,即
的函数,即
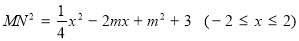 ,然后求最值使其等于1,注意分类讨论
,然后求最值使其等于1,注意分类讨论
(3)设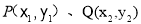 ,根据斜率之积是定值,
,根据斜率之积是定值, 在椭圆上,找出
在椭圆上,找出 坐标间的关系
坐标间的关系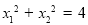 ;写出
;写出 所在直线方程
所在直线方程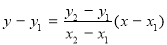 ,求
,求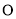 到直线
到直线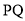 的距离
的距离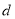 ,根据面积公式写出面积
,根据面积公式写出面积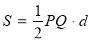 ,
,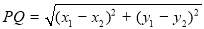
试题解析:【解析】
(1)设椭圆的方程为: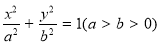 ,
,
由题意得: ,解得:
,解得: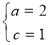 , 2分
, 2分
∴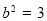 ,∴椭圆的标准方程:
,∴椭圆的标准方程: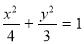 ; 4分
; 4分
(2)设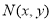 ,则
,则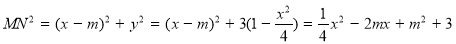
对称轴: ,
,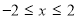 6分
6分
①当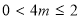 ,即
,即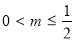 ,
, 时,
时,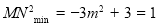 ,
,
解得: ,不符合题意,舍; 8分
,不符合题意,舍; 8分
②当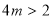 ,即
,即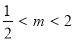 ,
,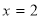 时,
时, ,
,
解得: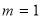 或
或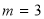 ;
;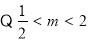
 ;
;
综上: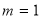 ,
,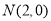 ; 10分
; 10分
(3)由题意得:四条垂线的方程为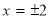 ,
,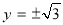 ,则
,则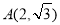 ,
,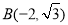
∴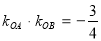
设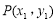 ,
,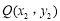 ,则
,则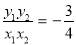 ①,
①,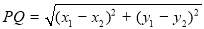 .
.
∵点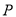 、
、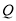 在椭圆C上 ∴
在椭圆C上 ∴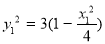 ,
,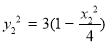
平方①得: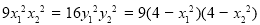 ,即
,即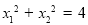 . 12分
. 12分
①若 ,则
,则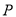 、
、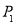 、
、 、
、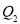 分别是直线
分别是直线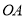 、
、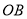 与椭圆的交点,∴四个点的坐标为:
与椭圆的交点,∴四个点的坐标为:
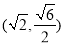 ,
,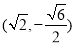 ,
,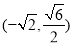 ,
,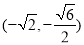 ∴四边形
∴四边形 的面积为
的面积为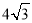 ;
;
②若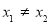 ,则直线
,则直线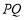 的方程可设为:
的方程可设为: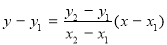 ,化简得:
,化简得:
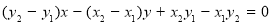 ,
,
所以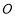 到直线
到直线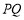 的距离为
的距离为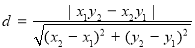 , 14分
, 14分
所以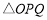 的面积
的面积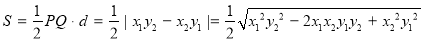
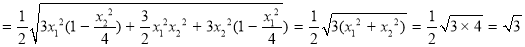 .
.
根据椭圆的对称性,故四边形 的面积为
的面积为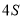 ,即为定值
,即为定值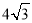 .
.
综上:四边形 的面积为定值
的面积为定值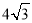 . 16分
. 16分
考点:直线与椭圆的最值定值问题

 的前n项和为
的前n项和为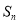 ,且4
,且4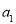 ,2
,2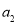 ,
,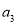 成等差数列。若
成等差数列。若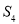 =( )
=( ) 满足
满足 ,若
,若 ,则a2016=
,则a2016= B.
B. C.
C. D.
D.
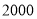 名运动员的年龄情况,从中抽取
名运动员的年龄情况,从中抽取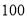 名运动员;就这个问题,下列说法中正确的有 ;
名运动员;就这个问题,下列说法中正确的有 ; 
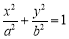
 的右焦点为
的右焦点为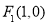 ,离心率为
,离心率为 .设A,B为椭圆上关于原点对称的两点,
.设A,B为椭圆上关于原点对称的两点, 的中点为M,
的中点为M, 的中点为N,原点
的中点为N,原点 在以线段
在以线段 为直径的圆上.设直线AB的斜率为k,若
为直径的圆上.设直线AB的斜率为k,若 ,则
,则
 的焦点恰好是双曲线
的焦点恰好是双曲线 的右焦点,则双曲线的渐近线方程为 .
的右焦点,则双曲线的渐近线方程为 . 为经过抛物线
为经过抛物线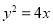 焦点的弦,且
焦点的弦,且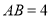 ,O为坐标原点,则
,O为坐标原点,则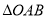 的面积等于_________.
的面积等于_________. ,若
,若
 ,则
,则 ;
;