题目内容
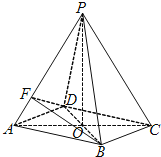
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 满足
满足![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() .
.
(![]() )当点
)当点![]() 是线段
是线段![]() 中点时,求直线
中点时,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)见解析;(3)直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】试题分析:(1)建立空间坐标系求两直线的方向向量,根据点积为0可证的结论;(2)求得直线的方向向量和面的法向量,证得两向量垂直即可;(3)求直线的方向向量和面的法向量的夹角即可.
解析:
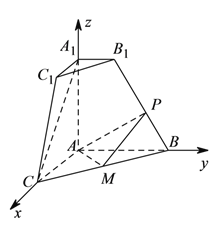
由已知可得, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,
![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
因为![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )证明:
)证明: ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
即![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴![]() .
.
(![]() )设
)设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
解得: ![]() ,
, ![]() ,
, ![]() ,即
,即![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,即
,即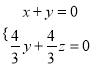 ,
,
令![]() ,则
,则![]() ,
, ![]() ,得
,得![]() .
.
又![]() ,
,
∴![]() .
.
∴直线![]() 平面
平面![]() .
.
(![]() )当点
)当点![]() 是线段
是线段![]() 中点时,
中点时, ![]() ,
,
设![]() 的一个法向量为
的一个法向量为![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,解
,解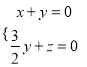 ,
,
令![]() ,则
,则![]() ,
, ![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
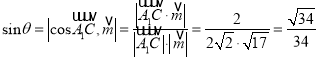 .
.
故直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
人员编号 | 1 | 2 | 3 | 4 | 5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
人员编号 | 6 | 7 | 8 | 9 | 10 |
(x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(1)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(2)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m﹣n,求随机变量ξ的分布列及其数学期望.