Question

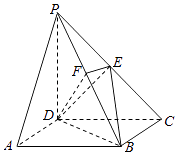
【题目】如图所示，在四棱锥中， 平面，底面是菱形， ， ， ． 为与的交点， 为棱上一点,

（1）证明：平面⊥平面；

（2）若三棱锥的体积为，

求证： ∥平面．

Answer 1

【答案】(1)见解析 (2) 见解析

【解析】试题分析：（1）要证明平面⊥平面，由面面垂直的判定定理知需在平面平面内找到一条直线垂直于另一个平面,通过分析后易知AC⊥平面PBD，再由线面垂直的判定定理即可证明.（2）由VP﹣EAD，需作出三棱锥的高，为此通过观察分析后，我们取AD中点H，连结BH，PH，在△PBH中，经点E作EF∥BH，交PH于点F,易证BH⊥平面PAD，再由EF∥BH，可得EF⊥平面PAD，故EF为三棱锥的高，

再由VP﹣EAD，可求出EF的值，又由∠BAD=60°，BH⊥AD，可求出BH的值，至此易知，即E为PB中点，而O为BD中点，所以OE为△PBD的中位线，由三角形中位线性质可得OE∥PD，再由线面平行判定定理PD∥平面EAC．

试题解析：

证明：（1）∵ABCD是菱形，∴AC⊥BD，

∵PD⊥底面ABCD，∴AC⊥PD，

∴AC⊥平面PBD，

又∵AC平面AEC，

∴平面AEC⊥平面PDB．

（2）取AD中点H，连结BH，PH，在△PBH中，经点E作EF∥BH，交PH于点F，

∵四边形ABCD是菱形，∠BAD=60°，

∴BH⊥AD，又BH⊥PD，AD∩PD=D，

∴BH⊥平面PAD，EF⊥平面PAD，

可得：BH=AB=，

∴VP﹣EAD=VE﹣PAD=SPAD×EF=

，

∴EF=，

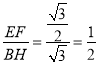∴，可得E为PB中点，

又∵O为BD中点，

∴OE∥PD，

∵PD平面EAC，OE平面EAC，

∴PD∥平面EAC．