Question

【题目】已知函数．

（Ⅰ）设曲线与轴正半轴交于点，求曲线在该点处的切线方程；

（Ⅱ）设方程有两个实数根，，求证：

Answer 1

【答案】（Ⅰ）（Ⅱ）见解析

【解析】

（Ⅰ）首先求出函数与轴正半轴交于点，求出函数的导函数即可得到即切线的斜率，最后利用点斜式求切线方程；

（Ⅱ）求出函数的单调区间，不妨设，则．首先证明：当时，，要证，只要证，即证．又，只要证，即证．令

利用导数研究函数的单调性从而得到，即可得证；

解：（Ⅰ）由，得．∴，即函数与轴正半轴交于点，

又因为．

∴．，

∴曲线在点处的切线方程为．

（Ⅱ）令得或．

且当或时；当时，．

∴的单调递增区间为，单调递减区间为，．

当或时；当时，．

不妨设，则．

下面证明：当时，．

当时，．

易知在上单调递增，

∴，即当时，．

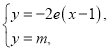由得．

记．

则．

要证，

只要证，即证．

又∵，∴只要证，即证．

∵，即证．

令，则．

当时，．为单调递减函数；

当时，．为单调递增函数．

∴，∴．

∴．