题目内容
3.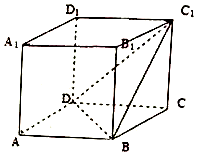 在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.
在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.(1)求证:平面ACC1A1⊥平面BDC1;
(2)求三棱锥D1-C1BD的体积.
分析 (1)连接AC交BD于O,由底面ABCD为菱形,得AC⊥BD,再由已知直四棱柱可得CC1⊥BD,由线面垂直的判定可得BD⊥平面ACC1A1,进一步得到平面ACC1A1⊥平面BDC1;
(2)由已知求出三角形DD1C1的面积,过点B作BH⊥CD交CD于H,则BH为三棱锥B-DD1C1的高,求出BH,再由等积法求得三棱锥D1-C1BD的体积.
解答 (1)证明:连接AC交BD于O,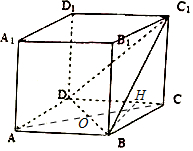
∵底面ABCD为菱形,∴AC⊥BD,
又ABCD-A1B1C1D1为直四棱柱,∴CC1⊥BD,
∵AC∩CC1=C,∴BD⊥平面ACC1A1,
∵BD?平面BDC1,∴平面ACC1A1⊥平面BDC1;
(2)解:由题知${V_{{D_1}-{C_1}BD}}={V_{B-D{D_1}{C_1}}}$,
又${S_{△D{D_1}{C_1}}}=\frac{1}{2}×2\sqrt{3}×4=4\sqrt{3}$,
过点B作BH⊥CD交CD于H,则BH为三棱锥B-DD1C1的高,且$BH=4sin60°=2\sqrt{3}$.
∴${V_{{D_1}-{C_1}BD}}={V_{B-D{D_1}{C_1}}}=\frac{1}{3}×2\sqrt{3}×4\sqrt{3}=8$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
11.椭圆$\frac{x^2}{4}+\frac{y^2}{9}=1$的长轴长为( )
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
18.已知下“斜二测”画法下,△ABC的直观图是一个边长为4的正三角形,则△ABC的面积为( )
| A. | $\sqrt{6}$ | B. | $8\sqrt{6}$ | C. | $16\sqrt{6}$ | D. | $4\sqrt{3}$ |