题目内容
8．若x，y满足$\left\{\begin{array}{l}x-y+2≤0\\ x+y-7≤0\\ x≥1\end{array}\right.$，则 $\frac{y}{x}$的取值范围是[$\frac{9}{5}$，6]．分析 先画出约束条件的可行域，然后分析$\frac{y}{x}$的几何意义，结合图象，用数形结合的思想，即可求解．
解答 解：满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x+y-7≤0\\ x≥1\end{array}\right.$的可行域，
如下图所示：
又∵$\frac{y}{x}$表示的是可行域内一点与原点连线的斜率
当x=$\frac{5}{2}$，y=$\frac{9}{2}$时，$\frac{y}{x}$有最小值$\frac{9}{5}$；
当x=1，y=6时，$\frac{y}{x}$有最大值6
故答案为：[$\frac{9}{5}$，6]
点评 平面区域的最值问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，分析表达式的几何意义，然后结合数形结合的思想，分析图形，找出满足条件的点的坐标，即可求出答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．已知过点（-2，0）的直线与圆O：x2+y2-4x=0相切与点P（P在第一象限内），则过点P且与直线$\sqrt{3}$x-y=0垂直的直线l的方程为（ ）
| A． | x+$\sqrt{3}$y-2=0 | B． | x+$\sqrt{3}$y-4=0 | C． | $\sqrt{3}$x+y-2=0 | D． | x+$\sqrt{3}$y-6=0 |
19．已知m是直线，α，β是两个互相垂直的平面，则“m∥α”是“m⊥β”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
16．“墨子号”是由我国完全自主研制的世界上第一颗空间量子科学实验卫星，于2016年8月16日发射升空．“墨子号”的主要应用目标是通过卫星中转实现可覆盖全球的量子保密通信．量子通信是通过光子的偏振状态，使用二进制编码，比如，码元0对应光子偏振方向为水平或斜向下45度，码元1对应光子偏振方向为垂直或斜向上45度．如图所示
信号发出后，我们在接收端将随机选择两种编码方式中的一种来解码，比如，信号发送端如果按编码方式1发送，同时接收端按编码方式1进行解码，这时能够完美解码；信号发送端如果按编码方式1发送，同时接收端按编码方式2进行解码，这时无法获取信息．如果发送端发送一个码元，那么接收端能够完美解码的概率是$\frac{1}{2}$；如果发送端发送3个码元，那么恰有两个码元无法获取信息的概率是$\frac{3}{8}$．
| 编码方式1 | 编码方式2 | |
| 码元0 |  |  |
| 码元1 |  |  |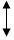
3．已知a，b∈R，则“b≠0”是“复数a+bi是纯虚数”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
13．某公司购买了A，B，C三种不同品牌的电动智能送风口罩．为了解三种品牌口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试它们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：
（Ⅰ）已知该公司购买的C品牌电动智能送风口罩比B品牌多200台，求该公司购买的B品牌电动智能送风口罩的数量；
（Ⅱ）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A品牌待机时长高于B品牌的概率；
（Ⅲ）再从A，B，C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a，b，c（单位：小时）．这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0．若μ0≤μ1，写出a+b+c的最小值（结论不要求证明）．
| A | 4 | 4 | 4.5 | 5 | 5.5 | 6 | 6 | |||
| B | 4.5 | 5 | 6 | 6.5 | 6.5 | 7 | 7 | 7.5 | ||
| C | 5 | 5 | 5.5 | 6 | 6 | 7 | 7 | 7.5 | 8 | 8 |
（Ⅱ）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A品牌待机时长高于B品牌的概率；
（Ⅲ）再从A，B，C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a，b，c（单位：小时）．这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0．若μ0≤μ1，写出a+b+c的最小值（结论不要求证明）．
17．i是虚数单位，复数$\frac{2+{i}^{3}}{1-i}$=（ ）
| A． | $\frac{3+i}{2}$ | B． | $\frac{1+3i}{2}$ | C． | $\frac{1+i}{2}$ | D． | $\frac{3+2i}{2}$ |
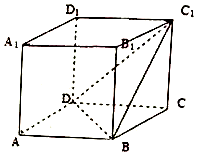在直四棱柱ABCD-A1B1C1D1中，AB=4，AA1=2$\sqrt{3}$，底面ABCD为菱形，且∠BAD=60°．