题目内容
19.已知函数f(x)=$\frac{1}{2}$x2-tcosx.若其导函数f′(x)在R上单调递增,则实数t的取值范围为( )| A. | [-1,-$\frac{1}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [-1,1] | D. | [-1,$\frac{1}{3}$] |
分析 求导数f′(x)=x+tsinx,并设g(x)=f′(x),并求出g′(x)=1+tcosx,由f′(x)在R上单调递增即可得出tcosx≥-1恒成立,这样即可求出t的取值范围.
解答 解:f′(x)=x+tsinx,设g(x)=f′(x);
∵f′(x)在R上单调递增;
∴g′(x)=1+tcosx≥0恒成立;
∴tcosx≥-1恒成立;
∵cosx∈[-1,1];
∴$\left\{\begin{array}{l}{-t≥-1}\\{t≥-1}\end{array}\right.$;
∴-1≤t≤1;
∴实数t的取值范围为[-1,1].
故选:C.
点评 考查基本初等函数的求导公式,函数的单调性和函数导数符号的关系.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.已知p:|x-1|<2,q:f(x)=$\frac{{x}^{2}+1}{x}$的最小值为2,则p是q的( )
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
14.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,0]}\\{{x}^{2}+2ax+1,x∈(0,+∞)}\end{array}\right.$,若函数g(x)=f(x)+2x-a有三个零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,-3) | D. | (0,-3) |
8.下列说法正确的是( )
| A. | 若命题p:?x0∈R,x02-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 已知相关变量(x,y)满足回归方程$\stackrel{∧}{y}$=2-4x,若变量x增加一个单位,则y平均增加4个单位 | |
| C. | 命题“若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,则实数m∈[0,1]为真命题 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
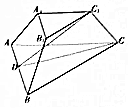 已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.
已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.