题目内容
10.已知元素为实数的集合S满足下列条件:①0∉S,1∉S;②若a∈S,则$\frac{1}{1-a}$∈S.(Ⅰ)若{2,-2}⊆S,求使元素个数最少的集合S;
(Ⅱ)若非空集合S为有限集,则你对集合S的元素个数有何猜测?并请证明你的猜测正确.
分析 (Ⅰ)利用①0∉S,1∉S;②若a∈S,则$\frac{1}{1-a}$∈S,求出集合的元素,即可得出结论;
(Ⅱ)非空有限集S的元素个数是3的倍数.与(Ⅰ)同法,即可证明结论.
解答 解:(Ⅰ)2∈S,则-1∈S,$\frac{1}{2}$∈S,可得2∈S;-2∈S,则$\frac{1}{3}$∈S,$\frac{3}{2}$∈S,可得-2∈S,
∴{2,-2}⊆S,使元素个数最少的集合S为{2,-1,$\frac{1}{2}$,-2,$\frac{1}{3}$,$\frac{3}{2}$}.------------------------(5分)
(Ⅱ)非空有限集S的元素个数是3的倍数.
证明如下:
(1)设a∈S则a≠0,1且a∈S,则$\frac{1}{1-a}$∈S,$\frac{1}{1-\frac{1}{1-a}}$=$\frac{a-1}{a}$∈S,$\frac{1}{1-\frac{a-1}{a}}$=a∈S
假设a=$\frac{1}{1-a}$,则a2-a+1=0(a≠1)m无实数根,故a≠$\frac{1}{1-a}$.
同理可证a,$\frac{1}{1-a}$,$\frac{a-1}{a}$两两不同.
即若有a∈S,则必有{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}⊆S.
(2)若存在b∈S(b≠a),必有{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}⊆S.{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$}∩{b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}=∅.
于是{a,$\frac{1}{1-a}$,$\frac{a-1}{a}$,b,$\frac{1}{1-b}$,$\frac{b-1}{b}$}⊆S.
上述推理还可继续,由于S为有限集,故上述推理有限步可中止,
∴S的元素个数为3的倍数.-------------------------------------------------------------(13分)
点评 本题考查新定义,考查集合元素的确定,难度大.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案| A. | 7+i | B. | 7-i | C. | 7+7i | D. | -7+7i |
| A. | -7 | B. | $-\frac{13}{4}$ | C. | -1 | D. | 7 |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
| A. | [-1,-$\frac{1}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [-1,1] | D. | [-1,$\frac{1}{3}$] |
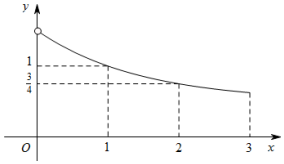 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1].
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1].