题目内容
已知数列{an}中，a1=0，an+1=an+2n-1（n∈N*），则数列{an}的通项公式是 ．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：利用累加法，然后把等式右边借助于等差数列的求和公式得答案．
解答：
解：由an+1=an+（2n-1），得
a2=a1+1．
a3=a2+3．
a4=a3+5．
…
an=an-1+（2n-3）．
累加得：an=a1+1+3+…+（2n-3）
=0+
=（n-1）2．
故答案为：an=（n-1）2．
a2=a1+1．
a3=a2+3．
a4=a3+5．
…
an=an-1+（2n-3）．
累加得：an=a1+1+3+…+（2n-3）
=0+
| (1+2n-3)(n-1) |
| 2 |
故答案为：an=（n-1）2．
点评：本题考查了数列递推式，考查了利用类加法求数列的通项公式，是中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
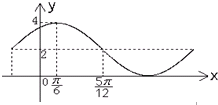已知函数y=Asin（ωx+φ）+B的一部分图象如图所示，如果