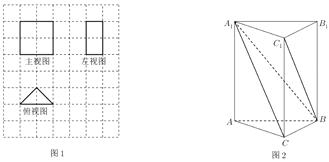
题目内容
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且满足
上,且满足![]() .
.
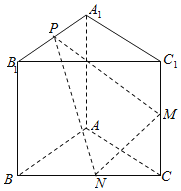
(1)证明:![]() .
.
(2)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,试确定P点的位置.
,试确定P点的位置.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)以AB,AC,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出各点的坐标及对应向量的坐标,易判断
,求出各点的坐标及对应向量的坐标,易判断![]() ,即
,即![]() ;(2)设出平面ABC的一个法向量,我们易表达出
;(2)设出平面ABC的一个法向量,我们易表达出![]() ,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的
,然后利用正弦函数的单调性及正切函数的单调性的关系,求出满足条件的![]() 值,进而求出此时
值,进而求出此时![]() 的正线值;(3)平面PMN与平面ABC所成的二面角为
的正线值;(3)平面PMN与平面ABC所成的二面角为![]() ,则平面PMN与平面ABC法向量的夹角余弦值的绝对值为
,则平面PMN与平面ABC法向量的夹角余弦值的绝对值为![]() ,代入向量夹角公式,可以构造一个关于
,代入向量夹角公式,可以构造一个关于![]() 的方程,解方程即可求出对应
的方程,解方程即可求出对应![]() 值,进而确定出满足条件的点P的位置.
值,进而确定出满足条件的点P的位置.
(1)证明:如图,以AB,AC,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,
从而![]() ,
,![]() ,
,
![]() ,
,
所以![]() .
.
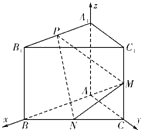
(2)平面ABC的一个法向量为![]() ,
,
则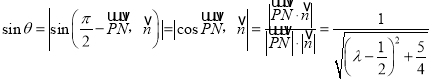 (※).
(※).
而![]() ,当
,当![]() 最大时,
最大时,![]() 最大,
最大,![]() 无意义,
无意义,![]() 除外,
除外,
由(※)式,当![]() 时,
时,![]() ,
,![]() .
.
(3)平面ABC的一个法向量为![]() .
.
设平面PMN的一个法向量为![]() ,
,
由(1)得![]() .
.
由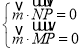 得
得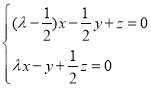 ,
,
解得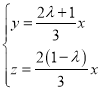 ,令
,令![]() ,得
,得![]() ,
,
∵平面PMN与平面ABC所成的二面角为![]() ,
,
∴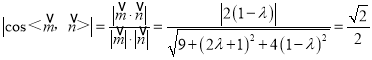 ,
,
解得![]() .
.
故点P在![]() 的延长线上,且
的延长线上,且![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目