题目内容
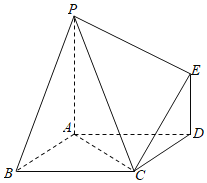
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
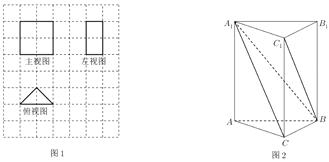
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
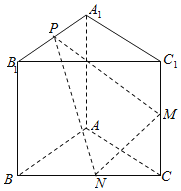
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
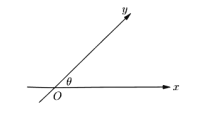
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
【答案】(1)2;(2)![]() ,arcsin
,arcsin![]() (或arccos
(或arccos![]() ).
).
【解析】
(1)由三视图还原原几何体,再由棱柱体积公式求解;
(2)阳马B﹣A1ACC1的体积V![]() A1A×AC×BC
A1A×AC×BC![]() AC×BC
AC×BC![]() (AC2+BC2)
(AC2+BC2)![]() AB2
AB2![]() ,当且仅当AC=BC
,当且仅当AC=BC![]() 时,
时,![]() ,以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,然后利用空间向量求解空间角.
,以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,然后利用空间向量求解空间角.
(1)由三视图还原原几何体如图,
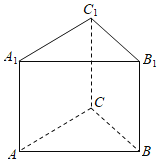
可知该几何体为直三棱柱,底面是等腰直角三角形,直角边长为![]() ,
,
直三棱柱的高为2,
则其体积为V![]() ;
;
(2)∵A1A=AB=2,阳马B﹣A1ACC1的体积:
V![]() A1A×AC×BC
A1A×AC×BC![]() AC×BC
AC×BC![]() (AC2+BC2)
(AC2+BC2)![]() AB2
AB2![]() ,
,
当且仅当AC=BC![]() 时,
时,![]() ,
,
以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,
则A1(0,![]() ,2),B(
,2),B(![]() ,0,0),C1(0,0,2),
,0,0),C1(0,0,2),
∴![]() (0,
(0,![]() ,2),
,2),![]() (
(![]() ,0,0),
,0,0),![]() (0,
(0,![]() ,0),
,0),![]() (
(![]() ,0,﹣2),
,0,﹣2),
设平面CA1B的法向量![]() (x,y,z),
(x,y,z),
则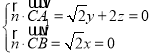 ,取y
,取y![]() ,得
,得![]() (0,
(0,![]() ,﹣1),
,﹣1),
设平面C1A1B的法向量![]() (a,b,c),
(a,b,c),
则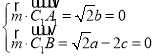 ,取a
,取a![]() ,得
,得![]() (
(![]() ,0,1),
,0,1),
设当阳马B﹣A1ACC1体积最大时,二面角C﹣A1B﹣C1的平面角为θ,
则cosθ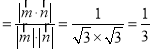 ,
,
∴当阳马B﹣A1ACC1体积最大时,二面角C﹣A1B﹣C1的大小为arccos![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目