题目内容
【题目】已知无穷数列![]() 的各项都不为零,其前n项和为
的各项都不为零,其前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,其中t为正整数.
,其中t为正整数.
![]() 求
求![]() ;
;
![]() 若不等式
若不等式![]() 对任意
对任意![]() 都成立,求首项
都成立,求首项![]() 的取值范围;
的取值范围;
![]() 若首项
若首项![]() 是正整数,则数列
是正整数,则数列![]() 中的任意一项是否总可以表示为数列
中的任意一项是否总可以表示为数列![]() 中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) 数列![]() 中的任意一项总可以表示为数列
中的任意一项总可以表示为数列![]() 中的其他两项之积.理由见解析.
中的其他两项之积.理由见解析.
【解析】
分析:(1)令![]() ,则
,则![]() ,即
,即![]() ,可得
,可得![]() .又由
.又由![]() 与
与![]() 的关系可得
的关系可得![]() ,从而数列
,从而数列![]() 是首项为
是首项为![]() ,公差为1的等差数列,由此可得
,公差为1的等差数列,由此可得![]() .(2)由
.(2)由![]() 可得数列
可得数列![]() 是首项为
是首项为![]() ,公差为1的等差数列;数列
,公差为1的等差数列;数列![]() 是首项为
是首项为![]() ,公差为1的等差数列,由此可得
,公差为1的等差数列,由此可得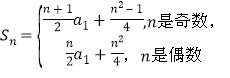 然后由题意讨论可得
然后由题意讨论可得![]() .(3)由(2)得数列
.(3)由(2)得数列![]() 的各项都是正整数.假设结论成立,即
的各项都是正整数.假设结论成立,即![]() ,即
,即![]() ,所以
,所以![]() ,取
,取![]() ,取
,取![]() ,故
,故![]() ,不妨设
,不妨设![]() 是偶数,则
是偶数,则![]() 一定是整数,讨论可得不论
一定是整数,讨论可得不论![]() 为奇数还是偶数,上式都有解,即假设成立.
为奇数还是偶数,上式都有解,即假设成立.
详解:(1)令![]() ,则
,则![]() ,即
,即![]() ,
,
又![]() ,
,
所以![]() ;
;
由![]() ,得
,得![]() ,
,
两式相减得![]() ,
,
又![]() ,
,
故![]() ,
,
所以![]() .
.
(2)由(1)知数列![]() 是首项为
是首项为![]() ,公差为1的等差数列;
,公差为1的等差数列;
数列![]() 是首项为
是首项为![]() ,公差为1的等差数列.
,公差为1的等差数列.
故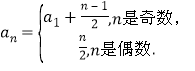
所以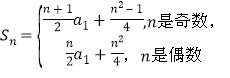
①当![]() 时奇数时,
时奇数时,![]() ,
,
即![]() ,
,
即![]() 对任意正奇数
对任意正奇数![]() 恒成立,
恒成立,
所以![]() ,
,
解得![]() .
.
②当![]() 时偶数时,
时偶数时,![]() ,
,
即![]() ,即
,即![]() 对任意正偶数
对任意正偶数![]() 恒成立,
恒成立,
所以![]() ,
,
解得![]() .
.
综合①②得![]() .
.
(3)由数列![]() 是首项为1,公差为1的等差数列;数列
是首项为1,公差为1的等差数列;数列![]() 是首项为正整数
是首项为正整数![]() ,公差为1的等差数列知,数列
,公差为1的等差数列知,数列![]() 的各项都是正整数.
的各项都是正整数.
设![]() ,即
,即![]() ,
,
所以![]() ,
,
取![]() ,取
,取![]() ,
,
故![]() ,
,
不妨设![]() 是偶数,则
是偶数,则![]() 一定是整数,
一定是整数,
故当![]() 是偶数时,方程
是偶数时,方程![]() 的一组解是
的一组解是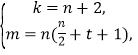
当![]() 是奇数时,方程
是奇数时,方程![]() 的一组解是
的一组解是
所以数列![]() 中的任意一项总可以表示为数列
中的任意一项总可以表示为数列![]() 中的其他两项之积.
中的其他两项之积.

练习册系列答案
相关题目