题目内容
12.已知x、y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,若x2+y2的最大值为m,最小值为n,则mx+ny的最小值为22.分析 作出不等式组对应的平面区域,利用点到直线的距离公式以及直线的截距的几何意义进行转化求解即可.
解答 解:作出不等式组对应的平面区域如图,
x2+y2的几何意义是区域内的点到原点的距离的平方,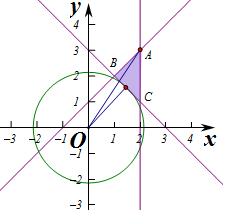
由图象知O到直线x+y-3=0的距离最小,
此时d=$\frac{|-3|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$,
则d2=$\frac{9}{2}$,即n=$\frac{9}{2}$,
OA的距离最大,
由$\left\{\begin{array}{l}{x=2}\\{x-y+1=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
则m=22+32=4+9=13,
则设z=mx+ny=13x+$\frac{9}{2}$y,
即y=-$\frac{26}{9}$x+$\frac{2}{9}$z,
平移直线y=-$\frac{26}{9}$x+$\frac{2}{9}$z,
由图象知当直线经过点B时,直线的截距最小,此时z最小,
由$\left\{\begin{array}{l}{x-y+1=0}\\{x+y-3=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即B(1,2),
此时z=13×1+$\frac{9}{2}$×2=13+9=22,
故答案为:22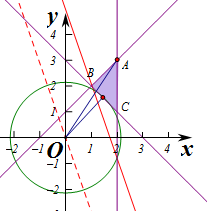 .
.
点评 本题主要考查线性规划的应用,结合点到直线的距离公式求出距离的最小值和最大值,以及利用直线的截距的几何意义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知平面区域D={(x,y)|$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$},Z=$\frac{y}{x+2}$.若命题“?(x,y)∈D,Z≥m”为真命题,则实数m的最大值为( )
| A. | $\frac{22}{15}$ | B. | $\frac{2}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
7.设全集U=R,集合A={x|x≥2},B={x|0≤x<6},则集合(∁UA)∩B=( )
| A. | {x|0<x<2} | B. | {x|0<x≤2} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
2.已知y2=4x抛物线,焦点记为F,过点F作直线l交抛物线于A,B两点,则$|{AF}|-\frac{2}{{|{BF}|}}$的最小值为( )
| A. | $2\sqrt{2}-2$ | B. | $\frac{5}{6}$ | C. | $3-\frac{3}{2}\sqrt{2}$ | D. | $2\sqrt{3}-2$ |
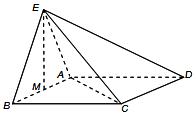 如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.