题目内容
已知二次函数f(x)=ax2-2bx+b(a≠0).
(1)若a∈{-2,-1,2},b∈{0,1},求满足f(1)>0的概率;
(2)若a∈(0,1),b∈(-1,1),求满足f(1)>0的概率.
(1)若a∈{-2,-1,2},b∈{0,1},求满足f(1)>0的概率;
(2)若a∈(0,1),b∈(-1,1),求满足f(1)>0的概率.
考点:几何概型,列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:(1)为古典概型,确定基本事件,可求满足f(1)>0的概率;
(2)为几何概型,计算面积,即可求满足f(1)>0的概率.
(2)为几何概型,计算面积,即可求满足f(1)>0的概率.
解答:
 解:(1)a∈{-2,-1,2},b∈{0,1},共有基本事件3×2=6个,
解:(1)a∈{-2,-1,2},b∈{0,1},共有基本事件3×2=6个,
满足f(1)>0,即a>b的有(2,0),(2,1)共2个,∴满足f(1)>0的概率为
=
;
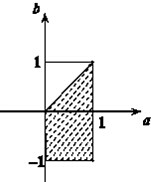
(2)如图所示,a∈(0,1),b∈(-1,1),对应区域的面积为1×2=2,
满足f(1)>0,即a>b的面积为2-
×1×1=
,
∴满足f(1)>0的概率为
.
 解:(1)a∈{-2,-1,2},b∈{0,1},共有基本事件3×2=6个,
解:(1)a∈{-2,-1,2},b∈{0,1},共有基本事件3×2=6个,满足f(1)>0,即a>b的有(2,0),(2,1)共2个,∴满足f(1)>0的概率为
| 2 |
| 6 |
| 1 |
| 3 |
(2)如图所示,a∈(0,1),b∈(-1,1),对应区域的面积为1×2=2,
满足f(1)>0,即a>b的面积为2-
| 1 |
| 2 |
| 3 |
| 2 |
∴满足f(1)>0的概率为
| 3 |
| 4 |
点评:本题考查等可能事件的概率,考查几何概型,解题的关键是确定概率模型、确定其测度.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 在三角形ABC中,点D分
在三角形ABC中,点D分