题目内容
已知命题p：x2-8x-20＜0，命题q：（x-m）（x-1-m）≥0，若?p是q的充分不必要条件，求实数m的取值范围．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：求出不等式对应的等价条件，利用充分不不必要的条件，即可得到结论．
解答：
解：由x2-8x-20＜0，得：-2＜x＜10，
?p：x≤-2或x≥10，
由（x-m）（x-1-m）≥0得：x≤m或x≥1+m，
依题意有?p⇒q但q⇒?p，
故
且等号不能同时成立，
解得-2≤m≤9．
即实数m的取值范围是[-2，9]．
?p：x≤-2或x≥10，
由（x-m）（x-1-m）≥0得：x≤m或x≥1+m，
依题意有?p⇒q但q⇒?p，
故
|
解得-2≤m≤9．
即实数m的取值范围是[-2，9]．
点评：本题主要考查一元二次不等式、不等式组的解法，简易逻辑的有关知识；考查运算求解的能力以及等价转化的思想．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
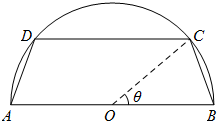一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，C，D在半圆上），设∠BOC=θ，木梁的体积为V（单位：m3），表面积为S（单位：m2）．