题目内容
直线l过抛物线x2=4y的焦点,则l被抛物线截得的弦的中点轨迹方程是 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:依题意,设过抛物线x2=4y的焦点F的直线l的方程为:y-1=kx,与x2=4y联立,可得x2-4kx-4=0,设l与抛物线x2=4y交点为A(x1,y1)、B(x2,y2)两点,AB的中点为M(x,y),利用韦达定理,可求得
,消掉参数k即可得到抛物线截得的弦的中点轨迹方程.
|
解答:
解:抛物线x2=4y的焦点F(0,1),则过焦点F的直线l的方程为:y-1=kx,
由
得:x2-4kx-4=0,
设l与抛物线x2=4y交于A(x1,y1)、B(x2,y2)两点,AB的中点为M(x,y),
则x1、x2为方程x2-4kx-4=0的两个根,
所以x1+x2=4k=2x,y1+y2=k(x1+x2)+2=4k2+2=2y,
整理得:
,消去k得:x2=2(y-1).
故答案为:x2=2(y-1).
由
|
设l与抛物线x2=4y交于A(x1,y1)、B(x2,y2)两点,AB的中点为M(x,y),
则x1、x2为方程x2-4kx-4=0的两个根,
所以x1+x2=4k=2x,y1+y2=k(x1+x2)+2=4k2+2=2y,
整理得:
|
故答案为:x2=2(y-1).
点评:本题考查抛物线的简单性质,考查直线与圆锥曲线的位置关系,考查韦达定理的应用与消参法,属于中档题.

练习册系列答案
相关题目
若抛物线y2=2px(p>0)上一点M到焦点F的距离为2p,则M点的横坐标为( )
| A、p | ||
| B、2p | ||
C、
| ||
D、
|
设双曲线
-
=1(m>0,n>0)的焦距为4
,一条渐近线方程为y=
x,则此双曲线的方程为( )
| x2 |
| m2 |
| y2 |
| n2 |
| 7 |
| 6 |
A、x2-
| ||||
B、
| ||||
| C、6x2-y2=1 | ||||
D、4x2-
|
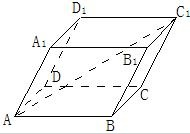 如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.
如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.