题目内容
1.从双曲线C:b2x2-a2y2=a2b2(a>0,b>0)的左焦点F1引圆x2+y2=a2的切线为l,切点为T,且l交双曲线的右支于点P,若点T满足$\overrightarrow{{F_1}T}=2\overrightarrow{TP}$,则双曲线C的离心率为$\sqrt{10}$.分析 化双曲线方程为标准式,作出图形,由已知利用平面几何知识把|F1P|、|F2P|都用含有b得代数式表示,代入双曲线定义即可求得双曲线C的离心率.
解答 解:双曲线C:b2x2-a2y2=a2b2(a>0,b>0)化为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0).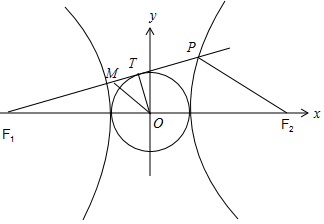
设双曲线的右焦点为F2,点M是线段F1P的中点,点O为坐标原点,
∴|F1T|=$\sqrt{|{F}_{1}O{|}^{2}-|OT{|}^{2}}$=$\sqrt{{c}^{2}-{a}^{2}}=b$.
∵$\overrightarrow{{F_1}T}=2\overrightarrow{TP}$,∴$|{F}_{1}P|=\frac{3}{2}|{F}_{1}T|=\frac{3}{2}b$,$|MT|=\frac{b}{4}$,$|{F}_{2}P|=2|OM|=2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}$.
由双曲线定义,|F1P|-|F2P|=2a,即$\frac{3}{2}b-2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}=2a$.
∴$\frac{3}{2}b-2a=2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}$,两边平方并整理得:$\frac{b}{a}=3$.
则$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=9$,e2=10.
∴$e=\frac{c}{a}=\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题考查双曲线的简单性质,考查了计算求解能力,是中档题.

练习册系列答案
相关题目
12.在如图所示的算法流程图中,输出S的值为( )
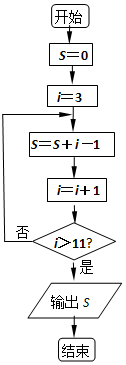

| A. | 51 | B. | 52 | C. | 53 | D. | 54 |
9. 《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )
《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )
 《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )
《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | -3 |
16.对某校高二年级某班63名同学,在一次期末考试中的英语成绩作统计,得到如下的列联表:
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参照附表,得到的正确结论是( )
| 不低于120分(优秀) | 低于120分(非优秀) | |
| 男 | 12 | 21 |
| 女 | 11 | 19 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过0.01的前提下认为“该班学生英语成绩优秀与性别有关” | |
| B. | 在犯错误的概率不超过0.05的前提下认为“该班学生英语成绩优秀与性别有关” | |
| C. | 没有90%以上的把握认为“该班学生英语成绩优秀与性别有关” | |
| D. | 有90%以上的把握认为“该班学生英语成绩优秀与性别有关” |
6.方程ρ=2cosθ表示的曲线是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
13.过点A(2,3)的直线的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=3+2t}\end{array}\right.$(t为参数),若此直线与直线x-y+3=0相交于点B,则|AB|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $\frac{3\sqrt{5}}{2}$ |
10.到一个三角形的三个顶点的距离的平方和最小的点,是这个三角形的( )
| A. | 垂心 | B. | 内心 | C. | 外心 | D. | 重心 |
11.在同一坐标系中,将曲线y=sinx通过φ:$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}$变换后的曲线是( )
| A. | y'=3sin2x' | B. | y'=3sin$\frac{x'}{2}$ | C. | y'=$\frac{1}{3}$sin2x' | D. | y'=$\frac{1}{3}sin\frac{x'}{2}$ |
