题目内容
设a、b、c均为正数,且a+b+c=1.证明:
(1) ab+bc+ca≤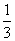 ;
;
(2) 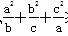 ≥1.
≥1.
证明:(1) 由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤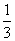 .
.
(2) 因为 +b≥2a,
+b≥2a, +c≥2b,
+c≥2b, +a≥2c,
+a≥2c,
故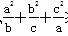 +(a+b+c)≥2(a+b+c),
+(a+b+c)≥2(a+b+c),
即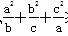 ≥a+b+c.
≥a+b+c.
所以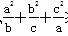 ≥1.
≥1.

练习册系列答案
相关题目
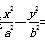 =1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=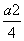 的切线,交双曲线右支于点P,切点为E,若
的切线,交双曲线右支于点P,切点为E,若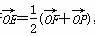 ,则双曲线的离心率为( )
,则双曲线的离心率为( )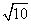 B.
B.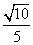
 D.
D.
 的最大值.
的最大值. .求△ABC在矩阵
.求△ABC在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (t为参数)相交于A、B两点,求|AB|.
(t为参数)相交于A、B两点,求|AB|.