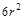题目内容
在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个圆的面积之和，则
sn=______．
| lim |
| n→∞ |
依题意可知，图形中内切圆半径分别为：r，r•cos30°，（r•cos30°）cos30°，（r•cos30°cos30°）cos30°，…，即内切圆半径组成以r为首项，
为公比的等比数列
∴圆的面积组成以πr2为首项，
为公比的等比数列
∴
Sn=
=4πr2
故答案为：4πr2．
| ||
| 2 |
∴圆的面积组成以πr2为首项，
| 3 |
| 4 |
∴
| lim |
| n→∞ |
| πr2 | ||
1-
|
故答案为：4πr2．
练习册系列答案
相关题目
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个圆的面积之和，则| lim |
| n→∞ |
| A、2πr2 | ||
B、
| ||
| C、4πr2 | ||
| D、6πr2 |
在半径为R的圆内作内接正方形，在这个正方形内作内切圆，又在圆内作内接正方形，如此无限次地作下去，试分别求所有圆的面积总和与所有正方形的面积总和．
如图，在半径为r的圆内作内接正六边形，再作正六边形的内切圆，又在此内切圆内作内接正六边形，如此无限继续下去，设Sn为前n个正六边形的面积之和，则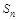
为前n 
B.
C.
D.