题目内容
2.已知f(x)=2x的反函数为g(x).h(x)=log4(3x+1),(1)若g(x+1)≥h(x),求x的取值范围D;
(2)令H(x)=h(x)-$\frac{1}{2}$g(x+1),当x∈D,求H(x)的值域.
分析 (1)先求出反函数的解析式及定义域,把解析式代入不等式,利用对数函数的单调性和定义域解此不等式;
(2)先利用对数的运算性质化简H(x)的解析式,再结合对数函数的图象与性质,从而解决问题.
解答 解:由y=2x得2x=y,∴x=log2y,
∴f-1(x)=log2x,(x>0),
即g(x)=log2x,(x>0),
(1)由g(x+1)≥h(x),得log2(x+1)≥log4(3x+1)
∴log4(x+1)2≥log4(3x+1)
∴$\left\{\begin{array}{l}x+1>0\\ 3x+1>0\\(x+1)^{2}≥3x+1\end{array}\right.$,
解得x∈$(-\frac{1}{3}$,0]∪[1,+∞),
∴D=$(-\frac{1}{3}$,0]∪[1,+∞);
(2)H(x)=h(x)-$\frac{1}{2}$g(x+1)=log4(3x+1)-$\frac{1}{2}$log2(x+1)=log4$\frac{3x+1}{x+1}$=log4(3-$\frac{2}{x+1}$),
∵x∈$(-\frac{1}{3}$,0]∪[1,+∞),
∴x+1∈($\frac{2}{3}$,1]∪[2,+∞),
∴$\frac{2}{x+1}$∈(0,1]∪[2,3),
∴3-$\frac{2}{x+1}$∈(0,1]∪[2,3),
∴log4(3-$\frac{2}{x+1}$)∈(-∞,0]∪[$\frac{1}{2}$,log43),
∴H(x)∈(-∞,0]∪[$\frac{1}{2}$,log43).
点评 本题考查反函数的求法和函数的值域,属于对数函数的综合题,要会求一些简单函数的反函数,掌握有关对数函数的值域的求法,属中档题.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | f(0)<f(-3)+f(2) | B. | f(0)=f(-3)+f(2) | C. | f(0)>f(-3)+f(2) | D. | 不确定 |
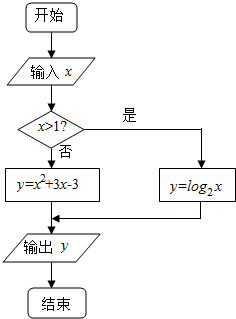
| A. | (-4,2]∪[2,+∞) | B. | [-4,1]∪[2,+∞) | C. | [-4,-2]∪{1}∪[4,+∞) | D. | (-∞,-4]∪{1}∪[2,+∞) |
 如图,在空间四边形ABCD中,E,F,G分别在棱AB,BC,CD上(与顶点不重合).
如图,在空间四边形ABCD中,E,F,G分别在棱AB,BC,CD上(与顶点不重合).