题目内容
3．已知实数a，b，c，d，e，f．a＜b＜c，d＜e＜f，（a-d）（a-e）（a-f）=-1，（b-d）（b-e）（b-f）=-1，（c-d）（c-e）（c-f）=-1，则a，b，c，d，e，f的大小关系是：a＜b＜c＜d＜e＜f；a＜b＜d＜c＜e＜f；a＜b＜d＜e＜c＜f；a＜d＜e＜b＜c＜f．分析 通过分类讨论，利用不等式的性质即可得出．
解答 解：①∵a＜b＜c，d＜e＜f，（c-d）（c-e）（c-f）=-1，
设c＜d，满足上式．
满足（a-d）（a-e）（a-f）=-1，（b-d）（b-e）（b-f）=-1，
∴a＜b＜c＜d＜e＜f．
②∵a＜b＜c，d＜e＜f，设b＜d＜c＜e，满足（a-d）（a-e）（a-f）=-1，（b-d）（b-e）（b-f）=-1，则（c-d）（c-e）（c-f）=-1，不成立；
同理可得：设b＜d＜e＜c＜f，成立．设b＜d＜e＜f＜c，不成立．
设a＜d＜b＜e，不成立．设a＜d＜e＜b＜c＜f，成立．
综上可得：a＜b＜c＜d＜e＜f；a＜b＜d＜c＜e＜f；a＜b＜d＜e＜c＜f；a＜d＜e＜b＜c＜f．
故答案为：a＜b＜c＜d＜e＜f；a＜b＜d＜c＜e＜f；a＜b＜d＜e＜c＜f；a＜d＜e＜b＜c＜f．
点评 本题考查了分类讨论、不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．已知集合A={x|x2-x-2≤0，x∈R}，B={x|lg（x+1）＜1，x∈Z}，则A∩B=（ ）
| A． | （0，2） | B． | [0，2] | C． | {0，2} | D． | {0，1，2} |
14．
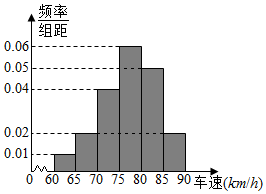对高速公路某段上汽车行驶速度进行抽样调查，画出如图频率分布直方图．根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率（ ）
对高速公路某段上汽车行驶速度进行抽样调查，画出如图频率分布直方图．根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率（ ）| A． | 75，0.25 | B． | 80，0.35 | C． | 77.5，0.25 | D． | 77.5，0.35 |
11．已知集合A={x|x≥4}，B={x|-1≤2x-1≤0}，则∁RA∩B=（ ）
| A． | （4，+∞） | B． | [0，$\frac{1}{2}$] | C． | （$\frac{1}{2}$，4） | D． | （1，4] |
18．已知31=3，32=9，33=27…，则32016的个位数上数字为（ ）
| A． | 1 | B． | 3 | C． | 7 | D． | 9 |
8．在如图所示的程序框图中，若输出的值是3，则输入x的取值范围是（ ）
| A． | （4，10] | B． | （2，+∞） | C． | （2，4] | D． | （4，+∞） |
12．已知A={-2，-1，0，1，2}，B={x|2x-1＞0}，则A∩B=（ ）
| A． | {-2，-1，0，1，2} | B． | {0，1，2} | C． | {0，1} | D． | {1，2} |
13．一个等差数列的前4项是a，x，b，2x，则$\frac{a}{b}$等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |