题目内容
4．直线x-y+m=0与圆x2+y2-2x-1=0有两个不同交点的一个必要不充分条件是（ ）| A． | 0＜m＜1 | B． | -4＜m＜0 | C． | m＜1 | D． | -3＜m＜1 |
分析 求出圆的标准方程，利用直线和圆相交的条件求出m的取值范围，结合充分条件和必要条件的定义进行判断即可．
解答 解：圆的标准方程为（x-1）2+y2=2，圆心为（1，0），半径r=$\sqrt{2}$，
若直线与圆有两个不同的交点，
则圆心到直线的距离d=$\frac{|1+m|}{\sqrt{2}}$$＜\sqrt{2}$，
即|1+m|＜2，得-2＜1+m＜2，得-3＜m＜1，
则-3＜m＜1的一个必要不充分条件是m＜1，
故选：C
点评 本题主要考查充分条件和必要条件的判断，利用直线和圆相交的等价条件求出m的取值范围是解决本题的关键．
练习册系列答案
相关题目
15．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A、B，上顶点为C，若△ABC是底角为30°的等腰三角形，则$\frac{c}{a}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
12．若角α的终边经过点P0（-3，-4），则tanα=（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | -$\frac{4}{5}$ | D． | -$\frac{3}{5}$ |
19．在△ABC中，角A、B、C的对边为a，b，c满足c=2acosBcosC+2bcosCcosA，且△ABC的面积为3$\sqrt{3}$，c=$\sqrt{13}$，则a+b=（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
16．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度后所得的函数图象过点P（0，1），则函数f（x）（ ）
| A． | 有一个对称中心$（{\frac{π}{12}，0}）$ | B． | 有一条对称轴$x=\frac{π}{6}$ | ||
| C． | 在区间$[{-\frac{π}{12}，\frac{5π}{12}}]$上单调递减 | D． | 在区间$[{-\frac{5π}{12}，\frac{π}{12}}]$上单调递增 |
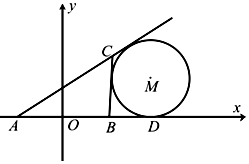如图所示，在△ABC中，AB的中点为O，且OA=1，点D在AB的延长线上，且$BD=\frac{1}{2}AB$．固定边AB，在平面内移动顶点C，使得圆M与边BC，边AC的延长线相切，并始终与AB的延长线相切于点D，记顶点C的轨迹为曲线Γ．以AB所在直线为x轴，O为坐标原点如图所示建立平面直角坐标系．
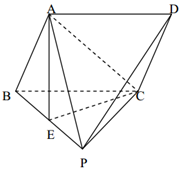如图，点P是平行四边形ABCD所在平面外一点，△PBC是等边三角形，点A在平面PBC的正投影E恰好是PB中点．