题目内容
11.椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点为F,斜率为1的直线l与椭圆交于A、B两点,当△FAB周长最大时,△FAB的面积为( )| A. | $\frac{12\sqrt{2}}{7}$ | B. | $\frac{2\sqrt{21}}{7}$ | C. | $\frac{6\sqrt{2}}{7}$ | D. | 3 |
分析 由椭圆方程求出左焦点坐标,设出直线l的方程,联立直线方程与椭圆方程,由判别式大于0求出m的范围,再由弦长公式和焦半径公式得到△FAB周长,由导数求得最大值,并得到此时m的值,进一步求得|AB|,由点到直线的距离公式求出F到l的距离,代入三角形面积公式得答案.
解答 解:由$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,知a2=4,b2=3,∴c2=a2-b2=1.
∴F(-1,0),
设直线l的方程为y=x+m,
联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得7x2+8mx+4m2-12=0.
由△=64m2-28(4m2-12)>0,得$-\sqrt{7}<m<\sqrt{7}$.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{8m}{7}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{7}$.
∴|AB|=$\sqrt{2}\sqrt{(-\frac{8m}{7})^{2}-4×\frac{4{m}^{2}-12}{7}}$=$\frac{4\sqrt{2}}{7}\sqrt{21-3{m}^{2}}$.
|AF|+|BF|=$2a+\frac{c}{a}({x}_{1}+{x}_{2})=4+\frac{1}{2}×(-\frac{8m}{7})$=$4-\frac{4m}{7}$.
∴△FAB周长为$\frac{4\sqrt{2}}{7}\sqrt{21-3{m}^{2}}+4-\frac{4m}{7}$.
令f(m)=$\frac{4\sqrt{2}}{7}\sqrt{21-3{m}^{2}}+4-\frac{4m}{7}$.
则f′(x)=$-\frac{4\sqrt{6}m+4\sqrt{7-{m}^{2}}}{7\sqrt{7-{m}^{2}}}$,由f′(x)=0,得m=-1.
∴当m=-1时,△FAB的周长有最大值.
此时|AB|=$\frac{24}{7}$,
直线l的方程为x-y-1=0.
则F到直线l的距离d=$\frac{|-1-1|}{\sqrt{2}}=\sqrt{2}$.
则△FAB的面积为$\frac{1}{2}×\frac{24}{7}×\sqrt{2}=\frac{12\sqrt{2}}{7}$.
故选:A.
点评 本题考查椭圆的简单性质,考查了直线和圆锥曲线位置关系的应用,训练了利用导数求最值,是中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件. |
| A. | 抛掷骰子试验 | |
| B. | 抛硬币 | |
| C. | 计算器 | |
| D. | 正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
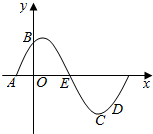 已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.
已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.