题目内容
18.二次函数y=-x2+4x一3的最大值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,先将二次函数y=-x2+4x一3的解析式变形为y=-(x-2)2+1,分析可得其最大值,即可得其答案.
解答 解:根据题意,y=-x2+4x一3=-(x2-4x+4)+1=-(x-2)2+1,
则其开口向下,其最大值为1;
故选:A.
点评 本题考查二次函数的性质与应用,注意结合二次函数的性质进行分析.

练习册系列答案
相关题目
11.椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点为F,斜率为1的直线l与椭圆交于A、B两点,当△FAB周长最大时,△FAB的面积为( )
| A. | $\frac{12\sqrt{2}}{7}$ | B. | $\frac{2\sqrt{21}}{7}$ | C. | $\frac{6\sqrt{2}}{7}$ | D. | 3 |
6.在等差数列{an}中,若a1=3,公差d≠0,则$\lim_{n→∞}$$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{{a}_{2}+{a}_{4}+…+{a}_{2n}}$的值( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 0 |
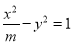 的实轴长是离心率的2倍,则m= .
的实轴长是离心率的2倍,则m= .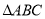 的外接圆为
的外接圆为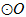 ,延长
,延长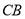 至
至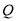 ,再延长
,再延长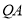 至
至 ,使得
,使得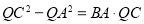 .
.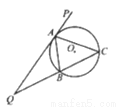
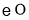 的切线;
的切线;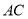 恰好为
恰好为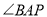 的平分线,
的平分线,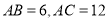 ,求
,求 的长度.
的长度.