题目内容
3.已知函数$f(x)={log_a}\frac{1-x}{1+x}$(a>0且a≠1)(1)若$f(-\frac{1}{3})=1$,集合A={x|f(x)=-2},B={1},写出集合A∪B的所有子集;
(2)若$f(-\frac{11}{13})=m$,$f(-\frac{7}{11})=n$,试用m,n来表示$f(-\frac{5}{7})$.
分析 (1)分别根据题中条件求出集合A,集合B,再求出A∪B及其全体子集;
(2)根据条件,先求出,${log_a}3=\frac{m+2n}{5}$,${log_a}2=\frac{2m-n}{5}$,再用m,n表示示$f(-\frac{5}{7})$.
解答 解:(1)由$f(-\frac{1}{3})=1$得,loga2=1,解得a=2,
再由${log_2}\frac{1-x}{1+x}=-2={log_2}\frac{1}{4}$得,$\frac{1-x}{1+x}=\frac{1}{4}$,解得,$x=\frac{3}{5}$,
因此,$A=\left\{{\frac{3}{5}}\right\}$,$A∪B=\left\{{\frac{3}{5},1}\right\}$,
∴A∪B的所有子集为:ϕ,$\left\{{\frac{3}{5}}\right\},\left\{1\right\}$,$\left\{{\frac{3}{5},1}\right\}$;
(2)由$f(-\frac{11}{13})=m$得,loga12=m,
即loga3+2loga2=m,-----------①
再由$f(-\frac{7}{11})=n$得,${log_a}\frac{9}{2}=n$
即2loga3-loga2=n,-----------②
联立①②解得,${log_a}3=\frac{m+2n}{5}$,${log_a}2=\frac{2m-n}{5}$,
所以,$f(-\frac{5}{7})={log_a}6={log_a}3+{log_a}2$=$\frac{3m+n}{5}$.
点评 本题主要考查了对数的图象与性质,对数的运算性质,以及子集的概念和集合的运算,属于中档题.

| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元 | 5 |
| 2 | 500~2000元 | 10 |
| 3 | 2000~5000元 | 15 |
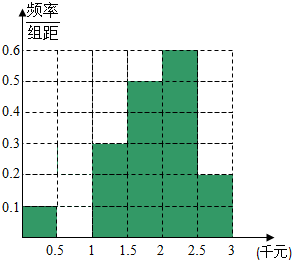 2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.
2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达3.32亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为0.4.| 网购金额 (单位:元) | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.30 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
(Ⅱ)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
| 网龄3年以上 | 网龄不足3年 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
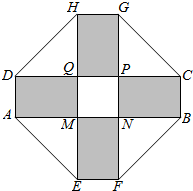 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.