题目内容
16.定义在非零实数集上的函数f(x)满足:f(xy)=f(x)+f(y),且f(x)在区间(0,+∞)上为递增函数.(1)求f(1)、f(-1)的值;
(2)求证:f(x)是偶函数;
(3)解不等式$f(2)+f(x-\frac{1}{2})≤0$.
分析 (1)利用赋值法即可求f(1)、f(-1)的值;
(2)根据函数奇偶性的定义即可证明f(x)是偶函数;
(3)根据函数奇偶性,利用数形结合即可解不等式$f(2)+f(x-\frac{1}{2})≤0$.
解答 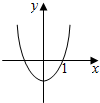 解:(1)令x=y=1,则f(1)=f(1)+f(1),
解:(1)令x=y=1,则f(1)=f(1)+f(1),
∴f(1)=0…(2分)
令x=y=-1,则f(1)=f(-1)+f(-1),
∴f(-1)=0…(4分)
(2)令y=-1,则f(-x)=f(x)+f(-1)=f(x),…(6分)
∴f(-x)=f(x)…(7分)
∴f(x)是偶函数 …(8分)
(3)根据题意可知,函数y=f(x)的图象大致如右图:
∵$f(2)+f(x-\frac{1}{2})=f(2x-1)≤0$,…(9分)
∴-1≤2x-1<0或0<2x-1≤1,…(11分)
∴$0≤x<\frac{1}{2}$或$\frac{1}{2}<x≤1$…(12分)
点评 本题主要考查抽象函数的应用以及函数奇偶性的判断,利用赋值法是解决本题的关键.

练习册系列答案
相关题目
7.设不等式组$\left\{\begin{array}{l}{x-y+4≤0}\\{x+y-2≤0}\\{y-2≥0}\\{\;}\end{array}\right.$示的平面区域为D.若指数函数y=ax(a>0且a≠1)的图象经过区域D上的点,则a的取值范围是( )
| A. | [$\sqrt{2}$,3] | B. | [3,+∞) | C. | (0,$\frac{1}{3}$] | D. | [$\frac{1}{3}$,1) |
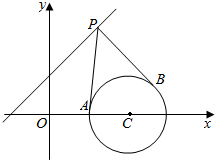 已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;
已知直线x-y+2=0和圆C:x2+y2-8x+12=0,过直线上的一点P(x0,y0)作两条直线PA,PB与圆C相切于A,B两点.①当P点坐标为(2,4)时,求以PC为直径的圆的方程,并求直线AB的方程;