题目内容

函数y=log
1
2
sin（2x+
π
4
）的单调递减区间为（　　）
A、（-
π
4
+kπ，kπ]，k∈Z
B、（-
π
8
+kπ，
π
8
+kπ]，k∈Z
C、（-
3π
8
+kπ，
π
8
+kπ]，k∈Z
D、（
π
8
+kπ，
3π
8
+kπ]，k∈Z
考点：复合函数的单调性
专题：函数的性质及应用
分析：根据复合函数单调性之间的关系即可得到结论．
解答： 解：由sin（2x+
π
4
）＞0，即2kπ＜2x+
π
4
＜2kπ+π，解得（-
π
8
+kπ，
3π
8
+kπ），k∈Z，
即函数的定义域为（-
π
8
+kπ，
3π
8
+kπ），k∈Z，
设t=sin（2x+
π
4
），则函数y=log
1
2
t为减函数，
要求函数y=log
1
2
sin（2x+
π
4
）的单调递减区间，根据复合函数单调性之间的关系，即求函数t=sin（2x+
π
4
）的增区间，
由2kπ＜2x+
π
4
＜2kπ+
π
2
，解得-
π
8
+kπ＜x＜
π
8
+kπ，k∈Z，
函数y=log
1
2
sin（2x+
π
4
）的单调递减区间（-
π
8
+kπ，
π
8
+kπ]，k∈Z，
故选：B
点评：本题主要考查函数单调区间的求解，根据复合函数单调性之间的关系以及三角函数的单调性是解决本题的关键．
练习册系列答案
相关题目
6个人排成一行，其中甲、乙两人不相邻的不同排法共有（　　）
A、
A
4
4
A
2
3
B、
A
4
4
C
2
5
C、
A
4
4
A
2
5
D、44
A
2
5
已知a=log0.31.8，b=log0.32.7，c=0.8-0.1，则（　　）
A、a＜b＜c
B、b＜a＜c
C、b＜c＜a
D、c＜a＜b
若函数y=f（x）在R上单调递增，且f（m2+1）＞f（-m+1），则实数m的取值范围是（　　）
A、（-∞，-1）
B、（0，+∞）
C、（-1，0）
D、（-∞，-1）∪（0，+∞）
已知集合M={1，（m2-3m-1）+（m2-5m-6）i}，N={1，3}，M∩N={1，3}，则实数m的值为（　　）
A、4B、-1
C、4或-1D、1或6
在（
x
+
2
x
）n的二项式展开式中，只有第5项的二项式系数最大，则n=（　　）
A、6B、7C、8D、9
正方体的外接球和内切球的表面积之比为（　　）
A、
3
：1
B、3
3
：1
C、3：1
D、3：
3
已知a=log34，b=0.910，c=log20.8，则有（　　）
A、a＞b＞c
B、b＞a＞c
C、c＞a＞d
D、b＞c＞a
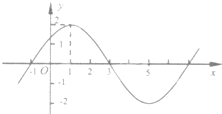已知函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜
π
2
）的图象的一部分如图所示．
（1）求函数f（x）的解析式；
（2）求函数f（x+2）的解析式，单调区间和最大（小）值及对应的x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网