题目内容
11.已知A,B,O三点不共线,若|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$+$\overrightarrow{OB}$|,则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为( )| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 锐角或钝角 |
分析 由向量的减法求得$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,两边平方($\overrightarrow{OB}-\overrightarrow{OA}$)2=($\overrightarrow{OA}$+$\overrightarrow{OB}$)2,展开得4$\overrightarrow{OA}•$$\overrightarrow{OB}$=0,即可求得两向量的夹角.
解答 解:$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,
|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$+$\overrightarrow{OB}$|,|$\overrightarrow{OB}-\overrightarrow{OA}$|=|$\overrightarrow{OA}$+$\overrightarrow{OB}$|,
∴($\overrightarrow{OB}-\overrightarrow{OA}$)2=($\overrightarrow{OA}$+$\overrightarrow{OB}$)2,
4$\overrightarrow{OA}•$$\overrightarrow{OB}$=0,
向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为$\frac{π}{2}$,
故答案为:B.
点评 本题考查向量的减法及求向量的夹角,属于基础题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
2.下列程序输出的结果是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
19.新学期开学之际,有A,B,C,D,E共5名同学同时考入某校高一年级,已知该校高一年级共有6个班,则每个班最多有这5名同学中的2名同学的不同情况共有( )
| A. | 4200种 | B. | 4320种 | C. | 6120种 | D. | 7920种 |
11.已知抛物线C:y2=6x的焦点为F,准线为l,点P在C上,点Q在l上,若$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则直线PQ的斜率为( )
| A. | ±1 | B. | ±$\sqrt{2}$ | C. | ±$\sqrt{3}$ | D. | ±2 |
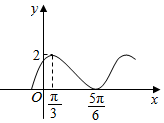 函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示. 下列程序在指定的正整数范围内所解的方程是x2-4x-5=0;输出的结果是5.
下列程序在指定的正整数范围内所解的方程是x2-4x-5=0;输出的结果是5.