题目内容
8.在锐角△ABC中,内角A、B、C的对边分别为a,b,c,已知a+2b=4,asinA+4bsinB=6asinBsinC,则△ABC的面积的最小值为$\frac{2}{3}$.分析 根据正弦定理化简已知的式子,由面积公式可得a2+4b2=12S,运用条件和基本不等式求出S的最小值.
解答 解:由正弦定理知,asinA+4bsinB=6asinBsinC即为a2+4b2=6absinC,
因为S=$\frac{1}{2}$absinC,所以a2+4b2=12S,
由a+2b=4得,a2+4b2=(a+2b)2-4ab=16-4ab,
则4ab=16-12S,
因为4ab≤2($\frac{a+2b}{2}$)2=8,
所以16-12S≤8,解得S≥$\frac{2}{3}$,当且仅当a=2b=2,取得等号.
此时a=2、b=1,S取得最小值为$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查正弦定理及面积公式的运用,同时考查基本不等式的运用,考查化简、变形能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
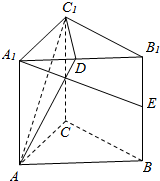 如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.
如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.