题目内容
2.一个游戏的规则如下:抛掷一枚质地均匀的骰子,若朝上的点数是1,则你赢t元;若点数是2,3或者4,则你输2元;若点数是5或者6,则不输不赢.(1)若t=4,你(玩家)连续玩了三次游戏,求你不输钱的概率;
(2)如果玩一次游戏要对你(玩家)有利,求t的取值范围.
分析 (1)根据条件,抛掷一次骰子,赢4元的概率为$\frac{1}{6}$,输2元的概率为$\frac{1}{2}$,不输不赢的概率为$\frac{1}{3}$,记事件A=“玩家连玩三次,不输钱”,由此利用对立事件概率计算公式能求出玩家连玩三次,不输钱的概率.
(2)记玩一次游戏,玩家获得ξ,则ξ的可能取值为t,-2,0,分别求出相应的概率,从而求出Eξ,若玩一次游戏要对玩家的利,则Eξ》0,由此能求出t的范围.
解答 解:(1)根据条件,抛掷一次骰子,赢4元的概率为$\frac{1}{6}$,
输2元的概率为$\frac{1}{2}$,不输不赢的概率为$\frac{1}{3}$,
记事件A=“玩家连玩三次,不输钱”,
每次游戏之间可以视为独立,
∴玩家连玩三次,不输钱的概率:
P=1-P($\overline{A}$)=1-($\frac{1}{2}$)3-${C}_{3}^{2}(\frac{1}{2})^{2}(\frac{1}{3})$-${C}_{3}^{1}(\frac{1}{2})(\frac{1}{3})^{2}$=$\frac{11}{24}$.
(2)记玩一次游戏,玩家获得ξ,则ξ的可能取值为t,-2,0,
P(ξ=1)=t,
P(ξ=-2)=$\frac{3}{6}=\frac{1}{2}$,
P(ξ=0)=$\frac{2}{6}=\frac{1}{3}$,
∴ξ的分布列为:
| ξ | t | -2 | 0 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{1}{3}$ |
则Eξ=$\frac{1}{6}t-2×\frac{1}{2}+0×\frac{1}{3}$=$\frac{t}{6}-1>0$,解得t>6.
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,考查对立事件、古典概型等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查函数与方程思想、化归与转化思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
2.若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0有三条公切线,则m=( )
| A. | 21 | B. | 19 | C. | 9 | D. | -11 |
3.阅读程序框图,运行相应的程序,则输出的T值为( )


| A. | 22 | B. | 24 | C. | 39 | D. | 41 |
7.已知cos(θ+$\frac{π}{2}$)=$\frac{4}{5}$,-$\frac{π}{2}$<θ<$\frac{π}{2}$,则sin2θ的值等于( )
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{12}{25}$ | D. | $\frac{12}{25}$ |
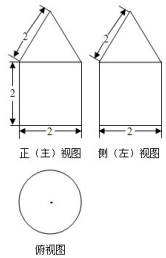 一个几何体的三视图如图所示:
一个几何体的三视图如图所示: