题目内容
20.已知函数f(x)=sin(ωx+φ)(ω>0)的图象关于直线x=$\frac{π}{16}$对称且f(-$\frac{π}{16}$)=0,如果存在实数x0,使得对任意的x都有f(x0)≤f(x)≤f(x0+$\frac{π}{4}$),则ω的最小值是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由题意直线x=是对称轴,对称中心为(-$\frac{π}{16}$,0),根据三角函数的性质可求ω的最小值.
解答 解:函数f(x)=sin(ωx+φ)(ω>0)的图象关于x=$\frac{π}{16}$对称且f(-$\frac{π}{16}$)=0,
∴ω$\frac{π}{16}$+φ=kπ+$\frac{π}{2}$…①,-ω$\frac{π}{16}$+φ=kπ…②,ωx0$\frac{ωπ}{4}$+φ≤$\frac{π}{2}$+2kπ且(ωx0+φ)≥-$\frac{π}{2}$+2kπ…③
由①②解得ω=4,φ=kπ+$\frac{π}{4}$,(k∈Z)
当k=0时,ω=4,φ=$\frac{π}{4}$,③成立,满足题意.
故得ω的最小值为4.
故选B.
点评 本题考查了三角函数图象及性质的综合运用能力和计算能力.属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
10.$\frac{1+3i}{1-i}$=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
11.有如图所示的程序框图,则该程序框图表示的算法的功能是( )
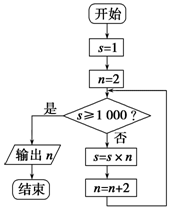

| A. | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B. | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C. | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D. | 输出使1×2×4×…×n≥1 000成立的最大整数n |
15.已知i是虚数单位,则$\frac{1+i}{1-i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
19.已知抛物线C:y2=4x的焦点为F,过点F且倾斜角为$\frac{π}{3}$的直线与抛物线C相交于P,Q两点,则弦PQ的长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{16}{3}$ |