题目内容
2.若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0有三条公切线,则m=( )| A. | 21 | B. | 19 | C. | 9 | D. | -11 |
分析 把圆的方程化为标准形式,分别求出圆心和半径,求出两圆的圆心距,利用圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0有三条公切线,可得圆心距等于两圆的半径和,即可得到结论.
解答 解:圆C1的方程:x2+y2=1,圆心C1(0,0),半径 为1,
圆C2:x2+y2-6x-8y+m=0,化为:(x-3)2+(y-4)2=25-m,圆心C2(3,4),半径为$\sqrt{25-m}$,
两圆的圆心距为5,
∵圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0有三条公切线,
∴5=1+$\sqrt{25-m}$,∴m=9,
故选:C.
点评 本题考查两圆的位置关系,两个圆的公切线的条数,注意圆心距与半径和与差的关系.

练习册系列答案
相关题目
12.已知数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}(0≤{a}_{n}<\frac{1}{2})}\\{2{a}_{n}-1(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,若a1=$\frac{6}{7}$,则a2011的值为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
13.执行如图所示程序框图,若输出的S值为-52,则条件框内应填写( )


| A. | i<4? | B. | i<6? | C. | i<5? | D. | i>5? |
10.$\frac{1+3i}{1-i}$=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
17.下列能正确反映《必修1》中指数幂的推广过程的是( )
| A. | 整数指数幂→有理数指数幂→无理数指数幂 | |
| B. | 有理数指数幂→整数指数幂→无理数指数幂 | |
| C. | 整数指数幂→无理数指数幂→有理数指数幂 | |
| D. | 无理数指数幂→有理数指数幂→整数指数幂 |
14.已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=1,$\overrightarrow{OP}$=t$\overrightarrow{OA}$,$\overrightarrow{OQ}$=(1-t)$\overrightarrow{OB}$,|$\overrightarrow{PQ}$|在t0时取最小值,当0<t0<$\frac{1}{4}$时,cosθ的取值范围为( )
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($\frac{1}{4}$,1) | D. | (-$\frac{1}{2}$,$\frac{1}{4}$) |
11.有如图所示的程序框图,则该程序框图表示的算法的功能是( )
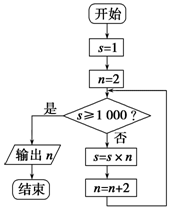

| A. | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B. | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C. | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D. | 输出使1×2×4×…×n≥1 000成立的最大整数n |
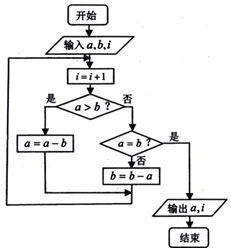 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )
如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )