题目内容
16.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0)关于直线y=$\frac{b}{c}$x的对称点Q在椭圆上,则椭圆的离心率是( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{3}{5}$ |
分析 设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.
解答 解:设Q(m,n),由题意可得$\left\{\begin{array}{l}{\frac{n}{m-c}=-\frac{c}{b}①}\\{\frac{n}{2}=\frac{b}{c}•\frac{m+c}{2}②}\\{\frac{{m}^{2}}{{a}^{2}}+\frac{{n}^{2}}{{b}^{2}}=1③}\end{array}\right.$,
由①②可得:m=$\frac{{c}^{3}-c{b}^{2}}{{a}^{2}}$,n=$\frac{2b{c}^{2}}{{a}^{2}}$,代入③可得:$\frac{(\frac{{c}^{3}-c{b}^{2}}{{a}^{2}})^{2}}{{a}^{2}}$+$\frac{(\frac{2b{c}^{2}}{{a}^{2}})^{2}}{{b}^{2}}$=1,
解得e2(4e4-4e2+1)+4e2=1,
可得,4e6+e2-1=0.
即4e6-2e4+2e4-e2+2e2-1=0,
可得(2e2-1)(2e4+e2+1)=0
解得e=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查椭圆的方程简单性质的应用,考查对称知识以及计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.△ABC的三边长分别为a,b,c,点D为BC边上的中点,下列说法正确的是( )
| A. | AD>$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | B. | AD=$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | ||
| C. | AD<$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ | D. | AD≤$\frac{1}{2}$$\sqrt{2({c}^{2}+{b}^{2})-{a}^{2}}$ |
7.若tanθ=$\frac{1}{3}$,则2cos2θ+sin2θ的值是( )
| A. | $\frac{12}{5}$ | B. | $\frac{8}{5}$ | C. | -$\frac{8}{5}$ | D. | -$\frac{12}{5}$ |
4.函数y=ln(x2)+x3的图象大致是( )
| A. | 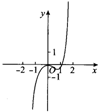 | B. | 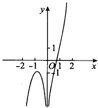 | C. | 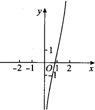 | D. | 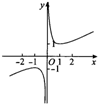 |