题目内容
14.一个袋中装有10个大小相同的黑球,白球和红球.已知从袋中任意摸出2个球,至少得到1个白球的概率是$\frac{7}{9}$.从袋中任意摸出3个球,记得到白球的个数为ξ,则随机变量ξ的数学期望Eξ=$\frac{3}{2}$.分析 设白球的个数为x,则红球和黑球的个数为10-x,记两个都不是白球的事件为A,
则至少有一个白球的事件与事件A为对立事件,由此求出白球的个数;
得出ξ的取值可能为0,1,2,3,求出ξ的分布列和数学期望.
解答 解:设白球的个数为x,则黑球和红球的个数为10-x;
记两个都不是白球的事件为A,则至少有一个白球的事件与事件A为对立事件;
所以p(A)=1-$\frac{7}{9}$=$\frac{2}{9}$=$\frac{{C}_{10-x}^{2}}{{C}_{10}^{2}}$,解得x=5,
所以白球的个数为5;
从袋中任意摸出3个球,到白球的个数ξ的取值可能为:0,1,2,3;
则P(ξ=0)=$\frac{{C}_{5}^{0}{•C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{1}{12}$,
P(ξ=1)=$\frac{{C}_{5}^{1}{•C}_{5}^{2}}{{C}_{10}^{3}}$=$\frac{5}{12}$,
P(ξ=2)=$\frac{{C}_{5}^{2}{•C}_{5}^{1}}{{C}_{10}^{3}}$=$\frac{5}{12}$,
P(ξ=3)=$\frac{{C}_{5}^{3}{•C}_{5}^{0}}{{C}_{10}^{3}}$=$\frac{1}{12}$,
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{5}{12}$ | $\frac{5}{12}$ | $\frac{1}{12}$ |
故答案为:$\frac{3}{2}$.
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.复平面上三点A、B、C分别对应复数1,2i,5+2i,则由A,B,C为顶点所构成的三角形是( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |
9.下列说法正确的是( )
| A. | 函数$y=sin(2x+\frac{π}{3})$在区间$(-\frac{π}{3},\frac{π}{6})$内单调递增 | |
| B. | 函数y=cos4x的最小正周期为2π | |
| C. | 函数y=cos(x+$\frac{π}{3}$)的图象是关于点($\frac{π}{6}$,0)成中心对称的图形 | |
| D. | 函数y=tan(x+$\frac{π}{3}$)的图象是关于直线x=$\frac{π}{6}$成轴对称的图形 |
3.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则三棱锥的体积为( )
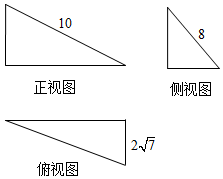

| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
2.一个盒子中共有12个大小相同的小球,其中红球9个,黄球3个,从盒子中任取3个球,将其中的红球染成黄色连同黄球一起放回,此时盒子中黄球的个数为ξ,则Eξ=( )
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |