题目内容
设命题p:
<0,命题q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要不充分条件,则实数a的取值范围是 .
| 2x-1 |
| x-1 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分别求出关于p,q的x的范围,结合¬p是¬q的必要不充分条件得到不等式组,从而求出a的范围.
解答:
解:由命题p:
<0,得:
<x<1,
由命题q:x2-(2a+1)x+a(a+1)≤0,得:a≤x≤a+1,
由¬p是¬q的必要不充分条件得:q是p的必要不充分条件,
∴
,解得:0≤a≤
,
故答案为:[0,
].
| 2x-1 |
| x-1 |
| 1 |
| 2 |
由命题q:x2-(2a+1)x+a(a+1)≤0,得:a≤x≤a+1,
由¬p是¬q的必要不充分条件得:q是p的必要不充分条件,
∴
|
| 1 |
| 2 |
故答案为:[0,
| 1 |
| 2 |
点评:本题考查了充分必要条件,考查了不等式的解法,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=sin(2x+φ),其中φ为实数,若f(
)=1,则函数g(x)=2cos(2x+φ)+1的单调递增区间是( )
| π |
| 3 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ-
|
设函数f(x)=
,则f(f(-1))的值为( )
|
| A、-2 | B、-1 | C、1 | D、2 |
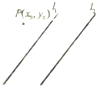 如图,点P(x0,y0)到直线l1:Ax+By+C=0,l2:Ax+By+C′=0(C≠C′)的有向距离分别为δ1=
如图,点P(x0,y0)到直线l1:Ax+By+C=0,l2:Ax+By+C′=0(C≠C′)的有向距离分别为δ1=| Ax0+By0+C | ||
|
| Ax0+By0+C′ | ||
|
A、0<
| ||||||
B、-1<
| ||||||
C、
| ||||||
D、
|