题目内容
若存在实数a,b(0<a<b)满足ab=ba,则实数a的取值范围是 .
考点:利用导数求闭区间上函数的最值,有理数指数幂的化简求值
专题:导数的综合应用
分析:0<a<b)满足ab=ba,由blna=alnb,化为
=
,令f(x)=
,(x>0),利用导数研究其单调性极值与最值,画出其图象即可得出.
| lna |
| a |
| lnb |
| b |
| lnx |
| x |
解答:
解:∵0<a<b)满足ab=ba,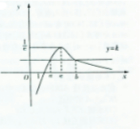
∴blna=alnb,化为
=
,
令f(x)=
,(x>0),
则f′(x)=
,
可得x>e时,f′(x)<0,此时函数f(x)单调递减;当0<x<e时,f′(x)>0,此时函数f(x)单调递增.
∴当x=e时,函数f(x)取得最大值,f(e)=
.
当x→0时,f(x)→-∞;当x→+∞时,f(x)→0.
∴当a∈(1,e)时,函数y=k与f(x)=
的图象有两个交点.
∴实数a的取值范围是(1,e),
故答案为:(1,e).

∴blna=alnb,化为
| lna |
| a |
| lnb |
| b |
令f(x)=
| lnx |
| x |
则f′(x)=
| 1-lnx |
| x2 |
可得x>e时,f′(x)<0,此时函数f(x)单调递减;当0<x<e时,f′(x)>0,此时函数f(x)单调递增.
∴当x=e时,函数f(x)取得最大值,f(e)=
| 1 |
| e |
当x→0时,f(x)→-∞;当x→+∞时,f(x)→0.
∴当a∈(1,e)时,函数y=k与f(x)=
| lnx |
| x |
∴实数a的取值范围是(1,e),
故答案为:(1,e).
点评:本题考查了利用导数研究其单调性极值与最值,考查了数形结合的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知F1,F2是双曲线
-
=1(a>0,b>0)的左右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||||
B、(
| ||||
C、(
| ||||
D、(1,
|
已知f(
x-1)=2x-5,且f(a)=6,则a等于( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
