题目内容
设函数f(x)是定义在R上的非常值函数,且对任意的x,y∈R有f(x+y)=f(x)f(y).
(1)证明:f(0)=1;
(2)设A={(x,y)|f(x2)f(y2)<f(1)},B={(x,y)|f(x+y+m)=1},若f(x)在R上是单调增函数,且A∩B=∅,求实数m的取值范围.
(1)证明:f(0)=1;
(2)设A={(x,y)|f(x2)f(y2)<f(1)},B={(x,y)|f(x+y+m)=1},若f(x)在R上是单调增函数,且A∩B=∅,求实数m的取值范围.
考点:抽象函数及其应用
专题:计算题,数形结合法
分析:(1)用特殊值法,在f(x+y)=f(x)f(y)中,令y=0得f(x)=f(x)•f(0),分析即可得f(0)=1,即得到证明;
(2)根据题意,分析f(x2)f(y2)<f(1)可得f(x2+y2)<f(1),进而结合函数的单调性由f(x2+y2)<f(1)可得x2+y2<1,又f(x+y+m)=1可得f(x+y+m)=f(0)?x+y+m=0,分析其几何意义,将其转化为直线与圆的位置关系,计算可得答案.
(2)根据题意,分析f(x2)f(y2)<f(1)可得f(x2+y2)<f(1),进而结合函数的单调性由f(x2+y2)<f(1)可得x2+y2<1,又f(x+y+m)=1可得f(x+y+m)=f(0)?x+y+m=0,分析其几何意义,将其转化为直线与圆的位置关系,计算可得答案.
解答:
解:(1)证明:
根据题意,在f(x+y)=f(x)f(y)中,令y=0得f(x)=f(x)•f(0),
又由f(x)不是常数,故f(0)=1;
(2)对于集合A={(x,y)|f(x2)f(y2)<f(1)},
由f(x+y)=f(x)f(y)可得f(x2+y2)<f(1),
又由f(x)在R上是单调增函数,则x2+y2<1,
可以看出集合A表示原点为圆心,1为半径的圆内部分(不包括边界),
对于集合B,由f(0)=1,
则f(x+y+m)=1?f(x+y+m)=f(0)?x+y+m=0,
集合B表示直线x+y+m=0,
若A∩B=∅,即直线与圆没有交点,
即A∩B=∅?
≥1.
解可得m≤-
或m≥
,
故m的取值范围是(-∞,-
]∪[
,+∞).
根据题意,在f(x+y)=f(x)f(y)中,令y=0得f(x)=f(x)•f(0),
又由f(x)不是常数,故f(0)=1;
(2)对于集合A={(x,y)|f(x2)f(y2)<f(1)},
由f(x+y)=f(x)f(y)可得f(x2+y2)<f(1),
又由f(x)在R上是单调增函数,则x2+y2<1,
可以看出集合A表示原点为圆心,1为半径的圆内部分(不包括边界),
对于集合B,由f(0)=1,
则f(x+y+m)=1?f(x+y+m)=f(0)?x+y+m=0,
集合B表示直线x+y+m=0,
若A∩B=∅,即直线与圆没有交点,
即A∩B=∅?
| |0+0+m| | ||
|
解可得m≤-
| 2 |
| 2 |
故m的取值范围是(-∞,-
| 2 |
| 2 |
点评:本题考查抽象函数的性质,涉及直线与圆的位置关系和集合的表示法,关键是分析集合元素的意义,将其转化为直线与圆的位置关系.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
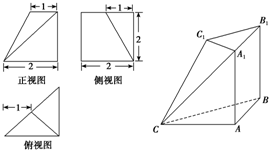
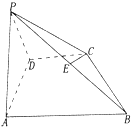 如图在四锥P-ABCD中,CD⊥平面PAD,CD∥AB,AB=2CD,PD=AD,E为PB中点.证明:
如图在四锥P-ABCD中,CD⊥平面PAD,CD∥AB,AB=2CD,PD=AD,E为PB中点.证明: