题目内容
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．已知两组技工在单位时间内加工的合格零件平均数都为9．
（1）分别求出m，n的值；
（2）分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s 
和s 
，并由此分析两组技工的加工水平；
（3）质检部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，若两人加工的合格零件个数之和大于17，则称该车间“质量合格”，求该车间“质量合格”的概率．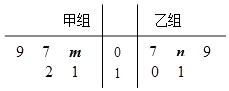 
【答案】
（1）解：∵两组技工在单位时间内加工的合格零件平均数都为9．
∴由茎叶图得： 
，
解得m=6，n=8
（2）解： 
= 
[（6﹣9）2+（7﹣9）2+（9﹣9）2+（11﹣9）2+（12﹣9）2]= 
．
= [（7﹣9）2+（8﹣9）2+（9﹣9）2+（10﹣9）2+（11﹣9）2]=2．
∵两组技工在单位时间内加工的合格零件平均数都为9， 
，
∴两组技工平均数相等，但乙组技工较稳定，故乙组技工加工水平高
（3）解：质监部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，
设两人加工的合格零件数分别为（a，b），
则所有的（a，b）有：
（6，7），（6，8），（6，9），（6，10），（6，11），（7，7），（7，8），（7，9），（7，10），
（7，11），（9，7），（9，8），（9，9），（9，10），（9，11），（11，7），（11，8），（11，9），
（11，10），（11，11），（12，7），（12，8），（12，9），（12，10），（12，11），共计25个，
而a+b≤17的基本事件有：
（6，7），（6，8），（6，9），（6，10），（6，11），（7，7），（7，8），（7，9），
（7，10），（9，7），（9，8），共计11个，
∴满足a+b＞17的基本事件共有14个，
∴该车间“质量合格”的基本事件有14个，
∴该车间“质量合格”的概率p= 
【解析】（1）由两组技工在单位时间内加工的合格零件平均数都为9．利用茎叶图能求出m，n．（2）先分别求出 ， ，由两组技工在单位时间内加工的合格零件平均数都为9， ，得到乙组技工加工水平高．（3）质监部门从该车间甲、乙两组技工中各随机抽取一名技工，对其加工的零件进行检测，设两人加工的合格零件数分别为（a，b），利用列举法能求出该车间“质量合格”的概率．
【考点精析】本题主要考查了茎叶图的相关知识点，需要掌握茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少才能正确解答此题．
