Question

【题目】已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若 =3 ，则|QF|= ， 点Q的坐标为 ．

Answer 1

【答案】；（ ，± ）
【解析】解：抛物线C：y2=8x的焦点为F（2，0），准线为l：x=﹣2，
=3 ，可得 = ，
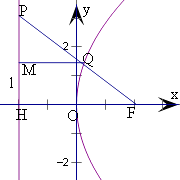
过Q作l的垂线，垂足为M，
设l与x轴的交点为H，
由三角形的相似可得，
= ，即为 = ，
则|QM|= ，
由抛物线的定义可得|QF|=|QM|= ；
又xQ+2= ，解得xQ= ，
yQ=± ．
即Q（ ，± ）．
故答案为： ，（ ，± ）．

求得抛物线的焦点F，准线l，运用向量共线定理和三角形的相似知识，可得|QM|= ，由抛物线的定义可得|QF|；运用点到直线的距离公式，解方程可得Q的坐标．