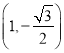Question

【题目】已知函数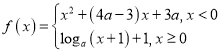(a＞0，且a≠1)在R上单调递减，且关于x的方程恰有两个不相等的实数解，则a的取值范围是

A．

B．

C．

D．

Answer 1

【答案】C

【解析】当时，f(x)单调递减，必须满足≥0，故0＜a≤，此时函数f(x)在[0，＋∞)上单调递减，若f(x)在R上单调递减，还需，即，所以．

结合函数图象，当x≥0时，函数y＝|f(x)|的图象和直线y＝2x有且只有一个公共点，即当x≥0时，方程|f(x)|＝2x只有一个实数解．因此，只需当x＜0时，方程|f(x)|＝2x恰有一个实数解．

根据已知条件可得，当x＜0时，f(x)＞0，即只需方程f(x)＝2x恰有一个实数解，即，即在(∞，0)上恰有唯一的实数解，

判别式，

因为，所以．

当3a2＜0，即a＜时，方程有一个正实根、一个负实根，满足要求；

当3a2＝0，即a＝时，方程的一个根为0，一个根为，满足要求；

当3a2＞0，即＜a＜时，因为 (2a1)＜0，此时方程有两个负实根，不满足要求；

当a=时，方程有两个相等的负实根，满足要求．

综上可知，实数a的取值范围是．故选C．