题目内容

精英家教网如图，在直角坐标系xOy中，设椭圆C：
x2
a2
+
y2
b2
=1?(a＞b＞0)的左右两个焦点分别为F1、F2．过右焦点F2且与x轴垂直的直线l与椭圆C相交，其中一个交点为M( 
2
，?1 )．
（1）求椭圆C的方程；
（2）设椭圆C的一个顶点为B（0，-b），直线BF2交椭圆C于另一点N，求△F1BN的面积．
分析：（1）由已知易得c值与线段MF2的长度，在直角三角形MF1F2中勾股定理求出a即可写出椭圆C的标准方程．
（2）此题可转化为求以线段为底边的两个三角形的和问题，一个三角形的高为b，另一个为|yn|．故只须求yn即可．
解答：解：（1）由椭圆定义可知|MF1|+|MF2|=2a．由题意|MF2|=1，
∴?|MF1|=2a-1．又由Rt△MF1F2可知(2a-1)2=(2
2
) 2+1，a＞0，
∴?a=2，又a2-b2=2，得b2=2．∴椭圆C的方程为
x2
4
+
y2
2
=1．
（2）直线BF2的方程为y=x-
2
．
由
y=x-
2
x2
4
+
y2
2
=1

得点N的纵坐标为
2
3
．又| F1F2 |=2
2
，
∴?S△F1BN=
1
2
×(
2
+
2
3
)×2
2
=
8
3
．
点评：考查求椭圆的方程，及椭圆中焦点三角形的面积，是直线与椭圆位置关系中一类相对来说比较简单点的题．
练习册系列答案
相关题目
（2009•杭州二模）如图，在直角坐标系xOy中，锐角△ABC内接于圆x2+y2=1．已知BC平行于x轴，AB所在直线方程为y=kx+m（k＞0），记角A，B，C所对的边分别是a，b，c．
（1）若3k=
2ac
a2+c2-b2
，求cos2
A+C
2
+sin2B的值；
（2）若k=2，记∠xOA=α(0＜α＜
π
2
)，∠xOB=β(π＜β＜
3π
2
)，求sin(α+β)的值．
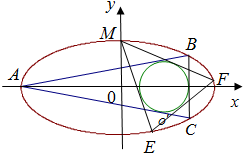精英家教网如图，在直角坐标系中，中心在原点，焦点在X轴上的椭圆G的离心率为e=
15
4
，左顶点A（-4，0），圆O'：（x-2）2+y2=r2是椭圆G的内接△ABC的内切圆．
（Ⅰ） 求椭圆G的方程；
（Ⅱ）求圆O'的半径r；
（Ⅲ）过M（0，1）作圆G的两条切线交椭圆于E，F两点，判断直线EF与圆O'的位置关系，并证明．
（2013•石景山区二模）如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且α∈(
π
6
，
π
2
)．将角α的终边按逆时针方向旋转
π
3
，交单位圆于点B．记A（x1，y1），B（x2，y2）．
（Ⅰ）若x1=
1
3
，求x2；
（Ⅱ）分别过A，B作x轴的垂线，垂足依次为C，D．记△AOC的面积为S1，△BOD的面积为S2．若S1=2S2，求角α的值．
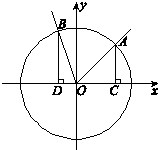精英家教网如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且α∈(
π
3
，
π
2
)．将角α的终边按逆时针方向旋转
π
6
，交单位圆于点B．记A（x1，y1），B（x2，y2）．
（Ⅰ）若x1=
1
4
，求x2； 
（Ⅱ）分别过A，B作x轴的垂线，垂足依次为C，D．记△AOC的面积为S1，△BOD的面积为S2．若S1=S2，求角α的值．
精英家教网如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：
3
x+3y=0（x≥0），过点P（a，0）（a＞0）作直线l分别交射线OA，OB于A，B两点，且
AP
=2
PB
，则直线l的斜率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网