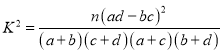题目内容
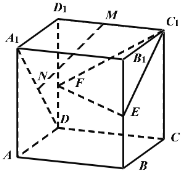
【题目】在正方体
中，点
是线段
上的动点，以下结论：
①
平面
；
②
；
③三棱锥
，体积不变；
④为中点时，直线
与平面所成角最大.
其中正确的序号为（ ）
A.①④B.②④C.①②③D.①②③④
【答案】D
【解析】
易证平面
平面
，可知
平面；正方体中
平面，可知平面
，
得证；由
平面
知
上点到平面的距离都相等，即棱锥底不变，高不变可得结论；根据线面角的定义知
，因为
为定值，即可判断
最短时，角最大.
如图，
,
,
，
平面平面，
又
平面，平面，①正确；
在正方体中易知平面，又平面平面，
所以平面，而
平面，所以，故②正确；
因为
,可知平面，所以上点到平面的距离都相等，
所以三棱锥
的体积不变，故③正确；
由③知，P运动时，P到平面的距离不变，设为，设直线与平面所成角为
，
则，当
为
中点时，最短，所以
最大，因为线面角
，
所以此时最大，故④正确.
故选：D
练习册系列答案
阅读快车系列答案
相关题目
