题目内容
【题目】线段AB为圆O的直径,点E,F在圆O上,AB//EF,矩形ABCD所在平面和圆O所在平面垂直,且![]() .则( )
.则( )
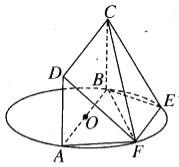
A.DF//平面BCE
B.异面直线BF与DC所成的角为30°
C.△EFC为直角三角形
D.![]()
【答案】BD
【解析】
四边形![]() 确定一个平面,
确定一个平面,![]() 不平行,说明
不平行,说明![]() 与平面
与平面![]() 有公共点,从而判断A选项;
有公共点,从而判断A选项;
连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,根据题设条件得出
,根据题设条件得出![]() 为等边三角形,异面直线BF与DC所成的角为
为等边三角形,异面直线BF与DC所成的角为![]() ,从而判断B选项;
,从而判断B选项;
求出![]() 三边的边长,根据勾股定理判断C选项;
三边的边长,根据勾股定理判断C选项;
根据棱锥的体积公式得出![]() ,即可判断D选项.
,即可判断D选项.
对A项,因为![]() ,
,![]() ,所以四边形
,所以四边形![]() 确定一个平面
确定一个平面
由于![]() 长度不相等,则
长度不相等,则![]() 不平行,即
不平行,即![]() 与平面
与平面![]() 有公共点,故A错误;
有公共点,故A错误;
对B项,连接![]() ,
,![]() 交
交![]() 于点
于点![]()
因为![]() ,
,![]() ,所以四边形
,所以四边形![]() 为菱形
为菱形
则![]() ,所以
,所以![]() 为等边三角形
为等边三角形
由于点![]() 为
为![]() 的中点,则
的中点,则![]()
因为![]() ,所以异面直线BF与DC所成的角为
,所以异面直线BF与DC所成的角为![]() ,故B正确;
,故B正确;
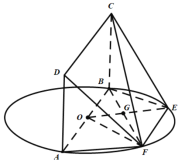
对C项,由于四边形![]() 为菱形,则
为菱形,则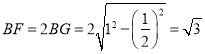
由面面垂直的性质以及线面垂直的性质可知,![]()
所以![]()
又![]() ,所以
,所以![]() 不是直角三角形,故C错误;
不是直角三角形,故C错误;
对D项,因为![]() ,
,![]() ,
,![]() ,所以
,所以
由面面垂直的性质可知,![]() 平面
平面![]() ,所以
,所以![]()
过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]()
根据面面垂直的性质可知![]() 平面
平面![]()
则![]()
即![]() ,故D正确;
,故D正确;

故选:BD

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目